Bias Correction for Forecasting PM2.5 Concentrations Using Measurement Data from Monitoring Stations by Region
Copyright © 2018 by Asian Journal of Atmospheric Environment
This is an open-access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The model and forecasting performances were evaluated to investigate the effectiveness of bias correction for forecasting PM2.5 concentrations for the period May 2012 to December 2014. Measured concentrations of PM2.5 and major components were obtained from five monitoring stations by region in the Korean Peninsula, and predicted concentrations were obtained from PM2.5 simulations using WRF model v3.4.1 and the CMAQ modeling system v4.7.1. Underestimation was prevalent at all stations for all components except NO3-. The effect of bias correction was pronounced at the Gangwon station, where the difference in PM2.5 between measured and predicted concentrations was largest. The performances for SO42- and the unresolved other component were primarily improved, whereas the performance for NO3-, which was originally overestimated, was degraded. The accuracy of the four-level forecast was moderate at 58% overall, but the probability of detection (POD) of high-concentration events was low at 23%. Bias correction improved the accuracy and POD to 68% and 52%, respectively; however, the rate of false detection of high-concentration events increased as well.
Keywords:
CMAQ/WRF, Major components, Mean fractional bias, Ratio adjustment, Forecasting performance1. INTRODUCTION
Concern about PM2.5 (particulate matter with an aerodynamic diameter of 2.5 μm or less) has prevailed over the Korean society in the last few years. High concentrations of 24-h PM2.5 exceeding 100 μg/m3 at the beginning of 2013 are presumed to have triggered public attention since they followed record-high 1-h averages approaching 1000 μg/m3 in Beijing (Shimadera et al., 2014; Wang et al., 2014; Zhang et al., 2014). Public worries were intensified when the International Agency for Research on Cancer (IARC, 2013) designated PM, as a representative outdoor air pollution, a Group 1 carcinogen in the same year. To meet the public demand for immediate information on PM, the Korean Government launched PM10 and PM2.5 forecasting in February 2014 and January 2015, respectively.
In Korea, three-dimensional numerical air quality models are used for PM forecasting. The air quality model predicts pollutant concentrations using emissions and meteorological data by specifying initial and boundary conditions. It is theoretically superior to the statistical model because it is based on physical and chemical understanding of atmospheric processes, whereas the latter is based on measurement data. We can construct a best initial field using all of the available data and can minimize the uncertainty of boundary conditions enough to enlarge the modeling domain for the air quality model. We can also obtain a fairly good set of meteorological data because the data-using system is well established, having a long history. However, forecasting using the air quality model cannot be more accurate than the emission data which should have restrictions in reproducing the real-world emissions. Furthermore, there is a big difference between model results, representing the mean of a grid that is several kilometers in length and width and several meters in height, and measurement data from a site installed in a densely populated area.
To improve the accuracy of the forecasting using the air quality model, the differences between model results and measurement data should be reduced, which could be accomplished by improving the models, by improving the input data such as emission data, and by correcting the model biases from measurement data. The first option is best in principle, but it takes considerable time and efforts. Although the second option is generally sought, it, like the first one, has limitations in reducing the aforementioned fundamental differences between model results and measurement data. The third option forces the model results closer to the measurement data. In the previous study, we investigated the differences in the model performance for measurement data from the intensive monitoring station in Seoul, and found that the ratio adjustment using mean values of model results and measurement data was the most effective of the three bias correction methods (Ghim et al., 2017).
In this study, we first examined the model performance for measurement data from five monitoring stations by region (Fig. 1) for three years from May 2012 to December 2014. Three stations in Seoul, Daejeon, and Gwangju are intensive monitoring stations and two stations in Ulsan and Chuncheon are comprehensive monitoring stations. Because the monitoring stations were distributed by region, we were able to estimate the regional characteristics of the model performance. Next, we examined the effects of bias correction on the model performance by station, applying the ratio adjustment method. Finally, we investigated whether the ratio adjustment method was also effective in improving the forecasting performance, as in the model performance.
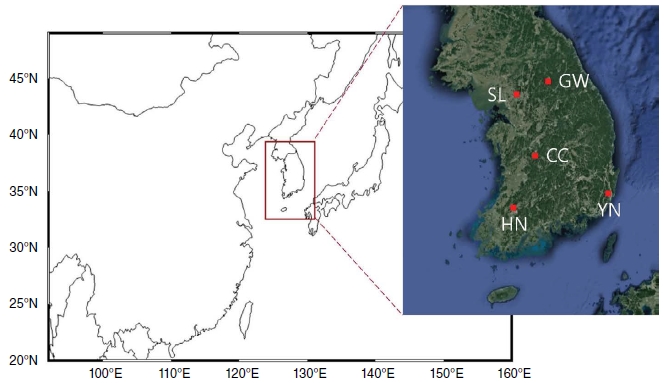
Modeling domain consisting of two grids with horizontal resolutions of 27 and 9 km. Five PM2.5 monitoring stations are shown on the fine grid: Seoul (SL) at Bulgwang in Seoul (126.93°E, 37.61°N), Chungcheong (CC) at Munhwa in Daejeon (127.41°E, 36.32°N), Honam (HN) at Oryong in Gwangju (126.85°E, 35.23°N), Yeongnam (YN) at Sinjeong in Ulsan (129.31°E, 35.53°N), and Gangwon (GW) at Seoksa in Chuncheon (127.75°E, 37.86°N).
2. METHODS
2. 1 Modeling
A three-dimensional air quality forecasting system consisting of Weather Research and Forecast (WRF) model v3.4.1 (Skamarock and Klemp, 2008), Sparse Matrix Operator Kernel Emissions Processor (SMOKE) v2.1 (http://www.smoke-model.org), and the Community Multiscale Air Quality (CMAQ) modeling system v4.7.1 (Byun and Schere, 2006) was used for PM2.5 simulation. WRF model simulations were initialized with Global Forecasting System (GFS) data sets. The WRF model results were prepared for daily emission processing and air quality simulations using the Meteorology–Chemistry Interface Processor. The Statewide Air Pollution Research Center version 99 (SAPRC99) and the fifth-generation modal aerosol model (AERO5) were used as the chemical mechanism and aerosol module, respectively, for the CMAQ simulation.
For anthropogenic emissions, the Intercontinental Chemical Transport Experiment-Phase B (INTEX-B) inventory for the year 2006 (Li et al., 2014; Zhang et al., 2009) was used for Northeast Asia, and the Clean Air Policy Support System (CAPSS) inventory for the year 2007 was used for Korea (Lee et al., 2011; Kim et al., 2008). Biogenic emissions were obtained using the Model of Emissions of Gases and Aerosols from Nature (MEGAN) version 2.04 (Guenther et al., 2006). Fig. 1 shows the modeling domain consisting of two grids with horizontal resolutions of 27 and 9 km. There were 15 layers vertically on a sigma coordinate up to 50 kPa with the lowest layer thickness of about 32 m. Default profiles provided with CMAQ were used as the boundary conditions for the coarse grid, and the boundary conditions for the fine grid were updated by the model outputs from the coarse grid.
2. 2 Measurements
PM2.5 samples were collected on a Teflon filter (Zefluor, Pall) using a well impactor ninety-six (WINS) and a sequential sampler (PMS-103, APM) at a flow rate of 16.7 L/min for 24 hours. Concentrations of PM2.5 and inorganic ions were measured using an automated filter weighing system (MTL) equipped with a microbalance (UMX2, Mettler Toledo) and ion chromatography (ICS 2000, Dionex), respectively. PM2.5 samples were also collected on a quartz filter (Tissuquartz 2500QAT-UP, Pall) to measure concentrations of organic and elemental carbons using an OCEC analyzer (Sunset). Concentrations of PM2.5 and its components were available on 460 days (47%) at Seoul (SL), 410 days (42%) at Chungcheong (CC), 456 days (47%) at Honam (HN), 329 days (34%) at Yeongnam (YN), and 288 days (30%) at Gangwon (GW), out of 975 days during the study period.
2. 3 Model Performance Metrics
The model performance was evaluated using mean fractional bias (MFB), correlation coefficient (R), and the slope and interceptor of best-fitted line between predicted and measured values. MFB is defined by
| (1) |
where pi and mi denote predicted and measured values, respectively, and N denotes the number of data (Boylan and Russell, 2006). We adopted the performance goals and criteria suggested by Boylan and Russell (2006), which denote the levels of accuracy that the best model can achieve and that are acceptable for standard model applications, respectively. They were given as:
| (2) |
where is (+)/2 in μg/m3, and and are the means of predicted and measured values, respectively.
2. 4 Forecasting Performance Statistics
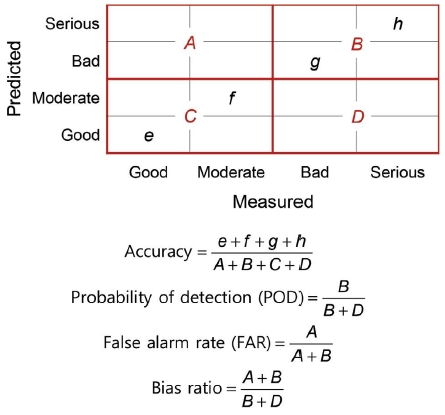
During the study period, PM2.5 concentrations were forecasted by dividing them into four levels as follows: good (≤15 μg/m3), moderate (15-50 μg/m3), bad (50-100 μg/m3), serious (>100 μg/m3). The forecasting performance was evaluated by examining whether the predicted level agreed with the measured level. We distinguished four groups from “A” to “D” and another four groups from “e” to “h” (Fig. 2). “A” indicates that low measured concentrations, which fall into either the good or moderate level, were predicted as high concentrations, which fall into either the bad or serious level. “B” indicates that high measured concentrations were correctly predicted. “e” to “h” indicates that each level was correctly predicted. Because both predicted and measured concentrations were divided into either high or low concentrations (in “A” to “D”), the sum of “A” to “D” is 100%.
We defined four parameters—the accuracy, probability of detection (POD), false alarm rate (FAR), and bias ratio—as shown in Fig. 2 (NIER, 2014; McKeen et al., 2005; USEPA, 2003). The accuracy is the percent of forecasts that correctly predicted the concentration levels. The remaining three parameters examine the quality of high-concentration forecasts. POD represents the ability to correctly predict high-concentration events, whereas FAR is the percent of high-concentration predictions that did not occur. The bias ratio is the ratio of predicted high-concentration events to observed high-concentration events. A bias ratio greater than 1 indicates that high-concentration events are overpredicted.
3. RESULTS AND DISCUSSION
3. 1 Model Performance
Fig. 3 compares the major components between measured and predicted concentrations by station. The measured PM2.5 concentration is lowest at YN and highest at GW. YN exhibits the lowest concentrations of major components except for the unresolved other component whose concentration is highest. At GW, the OC concentration is highest whereas the secondary ions are lowest except for YN. Underestimation of the predicted PM2.5 is remarkable at GW (Table 1), where the measured PM2.5 is highest. In Table 1, the ratio of predicted to measured concentration for NH4+ is close to one on the whole. However, the ratio for NO3- is greater than 1, and the ratios for carbonaceous components (OC and EC) are less than 0.3, indicating significant underestimation. For the major ions, the overestimation of NO3- at YN and the underestimation of SO42- at GW are notable. At GW, OC underestimation is serious, and EC is underestimated similarly to CC and HN. Despite a substantial overestimation of NO3- at YN, its effect on PM2.5 is insignificant because of a low proportion (Fig. 3). Given a prevalence of underestimations, the model performance is better at YN and SL because of high ratios of predicted to measured concentration for major components.
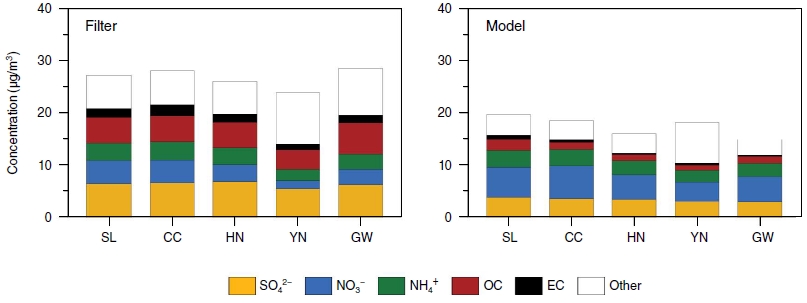
The mean values of measured and predicted concentrations of major components at monitoring stations by region. The sum of the components is PM2.5, and the other is the remainder of PM2.5 excluding the components shown in the figure.
3. 2 Bias Correction
Table 2 shows the differences in model performance metrics by station due to bias correction. The predicted concentrations become identical to the measured concentrations because the bias was corrected by multiplying the predicted concentration by the ratio of measured to predicted concentration (ratio adjustment). In contrast, R and the relative intercept remain unchanged. On the whole, the model performance was improved by the bias correction, as MFB moves within the goals from outside and the slope increases from 0.62 to 0.95. The effect of bias correction is noticeable at GW, where MFB moves within the goals from outside the criteria and the slope increases from the lowest at 0.47 to 0.89. At HN, MFB falls within the goals after correction, but its absolute value is still highest along with that at CC, and the slope increases above 1.0, indicating that the correction effect is unclear.
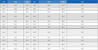
Differences in model performace metrics by station resulting from bias correction using PM2.5 mean values.
Table 3 shows the differences in MFB for major components. Overall, MFBs for SO42- and the other, which fall outside the criteria and goals, respectively, move within the goals. In contrast, MFB for NO3- is pushed outside the criteria because of the correction. MFBs for both OC and EC are improved, but are still outside the criteria. Looking into the differences by station, SO42- improves at all stations, as does the other at all stations except for YN where MFB originally fell within the goals. On the other hand, NO3- and NH4+ exhibit degradation at all stations; particularly, MFBs for NO3- at SL, CC and HN move outside the criteria, and MFB for NH4+ at GW moves outside the goals.
3. 3 Forecasting Performance
Fig. 4 shows a plot of predicted vs. measured concentrations for PM2.5 at all stations. Individual values are compared, different from comparing mean values in the previous sections to examine the model performance. Originally, more data points lie below the 1 : 1 line, indicating the tendency of underestimation of predicted concentrations (Fig. 4(a)). However, the data points move upward due to bias correction, and the amount of data whose predicted level coincides with the measured level increases, despite some overpredicted data points.
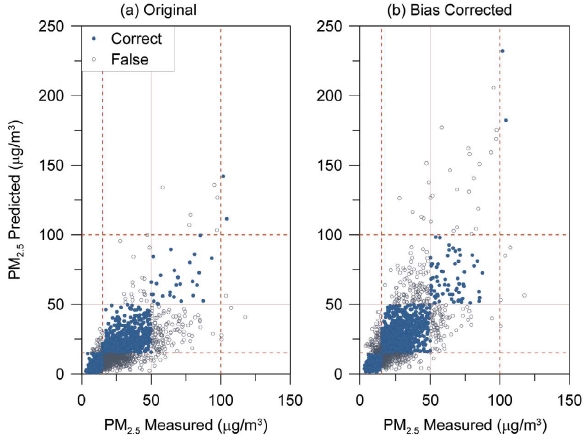
Plot of predicted vs. measured PM2.5 concentrations at all stations. Dotted lines denote the division of concentration levels, and solid lines denote the division of high and low concentrations (see Fig. 2 and the description in the text for details). “Correct” and “false” in the legend indicate that the predicted level coincides and does not coincide with the measured level, respectively. The biases were corrected using mean values by station in (b).
The differences in the forecasting performance statistics that resulted from bias correction are summarized in Table 4. Originally, the overall accuracy for all levels was moderate at 58%, but POD for high-concentration events was only 23% (Table 4(a)). FAR and the bias ratio are also low at 33% and 34%, respectively. High-concentration forecasts are generally fewer, particularly at GW, and consequently, high FAR and the bias ratio at YN are distinguished. Table 4(b) shows the bias corrected performances. Overall, the accuracy and POD increase by 10% and 30%, respectively, whereas FAR also increases to 56%. Most of all, because the frequency of high-concentration forecasts greatly increases, the bias ratios exceed 100% except for SL. By station, all four parameters at HN and GW greatly increase. The differences in performances between the stations are generally reduced by the bias correction, although a high value of POD at HN becomes even higher. A representative case is GW where FAR increases from 0% to 49%.

Differences in forecasting performance statisticsa (%) by station resulting from bias correction using PM2.5 mean values.
Note that mean values during the same period were used for bias correction, which cannot be accomplished in the real-time forecasting. However, we tested this bias correction because the effectiveness of bias correction using mean values did not depend much on the period of data used for the correction in our previous study (Ghim et al., 2017). It was probably because the biases of model results from measurement data in Korea were systematically caused by limitations in reproducing the atmospheric environment such as meteorology and emissions during model simulation. The present study revealed that the biases were specific to station (or region) and that the correction should be conducted by station (or region).
4. SUMMARY AND CONCLUSIONS
The model performances and forecasting performances were evaluated using mean and individual data, respectively, for PM2.5 and major components from five monitoring stations by region for the period May 2012 to December 2014. WRF model v3.4.1 and the CMAQ modeling system v4.7.1 were used for PM2.5 simulation. The effects of bias correction on the two performances were investigated in the second step.
MFB at GW fell outside the criteria because of the lowest predicted concentration despite having the highest measured concentration, whereas those at YN and SL were close to the goals. For the major components, MFBs for NH4+ at all stations fell within the goals. On the other hand, MFB for OC at all stations fell outside the criteria, and MFBs for EC and SO42- also performed poorly as they fell outside the criteria at many stations.
The effect of bias correction was pronounced at GW, which had the largest absolute MFB and the smallest slope of the best-fit line, but the performance was improved more than the average for the five stations after correction. In contrast, the effect of correction was unclear at HN, considering that the absolute MFB was still the largest with CC, and the slope increased above 1.0. The performances of SO42- and the unresolved other component were improved primarily, whereas the performance of NO3-, which was originally overestimated, was degraded.
The accuracy of the four-level forecast was moderate, at 58% overall; both POD and FAR were low at 23% and 33%, respectively. This tendency was particularly severe at GW, with a POD of 9.8% and a FAR of 0%. Overall, bias correction improved the accuracy and POD to 68% and 52%, respectively, but FAR also increased to 56%. In addition, the differences in performances between stations were generally reduced as POD and FAR at GW greatly increased.
Acknowledgments
This study was supported by the PM2.5 Research Center supported by the Ministry of Science, ICT, and Future Planning (MSIP) and the National Research Foundation (NRF) of Korea (NRF-2014M3C8A5030623), the National Strategic Project-Fine Particle of the National Research Foundation of Korea funded by the Ministry of Science and ICT, the Ministry of Environment, and the Ministry of Health and Welfare (2017M3D8A1092015), and the Hankuk University of Foreign Studies Research Fund.
References
-
Boylan, J.W., Russell, A.G., (2006), PM and light extinction model performance metrics, goals, and criteria for three-dimensional air quality models, Atmospheric Environment, 40, p4946-4959.
[https://doi.org/10.1016/j.atmosenv.2005.09.087]

-
Byun, D.W., Schere, K.L., (2006), Review of the governing equations, computational algorithms, and other components of the Models-3 Community Multiscale Air Quality (CMAQ) modeling system, Applied Mechanics Reviews, 59, p51-77.
[https://doi.org/10.1115/1.2128636]

- Ghim, Y.S., Choi, Y., Kim, S., Bae, C.H., Park, J., Shin, H.J., (2017), Model performance evaluation and bias correction effect analysis for forecasting PM2.5 concentrations, Journal of Korean Society for Atmospheric Environment, 33, p11-18, (in Korean with English abstract).
-
Guenther, A., Karl, T., Harley, P., Wiedinmyer, C., Palmer, P.I., Geron, C., (2006), Estimates of global terrestrial isoprene emissions using MEGAN (Model of emissions of gases and aerosols from nature), Atmospheric Chemistry and Physics, 6, p3181-3210.
[https://doi.org/10.5194/acpd-6-107-2006]

- IARC (International Agency for Research on Cancer), (2013), Outdoor air pollution a leading environmental cause of cancer deaths, Press Release No. 221.
- Kim, S., Moon, N., Byun, D.W., (2008), Korea emissions inventory processing using the US EPA’s SMOKE System, Asian Journal of Atmospheric Environment, 2, p34-46.
- Lee, D.G., Lee, Y.M., Jang, K.W., Yoo, C., Kang, K.H., Lee, J.H., Jung, S.W., Park, J.M., Kee, S.B., Han, J.S., Hong, J.H., Lee, S.J., (2011), Korean national emissions inventory system and 2007 Air pollutant emissions, Asian Journal of Atmospheric Environment, 5, p278-291.
-
Li, M., Zhang, Q., Streets, D.G., He, K.B., Cheng, Y.F., Emmons, L.K., Huo, H., Kang, S.C., Lu, Z., Shao, M., Su, H., Yu, X., Zhang, Y., (2014), Mapping Asian anthropogenic emissions of non-methane volatile organic compounds to multiple chemical mechanisms, Atmospheric Chemistry and Physics, 14, p5617-5638.
[https://doi.org/10.5194/acp-14-5617-2014]

-
McKeen, S., Wilczak, J., Grell, G., Djalalova, I., Peckham, S., Hsie, E.Y., Gong, W., Bouchet, V., Moffet, R., McHenry, J., McQueen, J., Tang, Y., Carmichael, G.R., Pagowski, M., Chan, A., Dye, T., Frost, G., Lee, P., Mathur, R., (2005), Assessment of an ensemble of seven real-time ozone forecasts over eastern North America during the summer of 2004, Journal of Geophysical Research, 110, pD21307.
[https://doi.org/10.1029/2005jd005858]

- NIER (National Institute of Environmental Research), (2014), Study on Optimization of the Forecasting Model for Particulate Matter, Prepared by Inha University, Enitech, and Yeungnam University, (in Korean).
- Shimadera, H., Hayami, H., Ohara, T., Morino, Y., Takami, A., Irei, S., (2014), Numerical simulation of extreme air pollution by fine particulate matter in China in Winter 2013, Asian Journal of Atmospheric Environment, 8, p25-34.
-
Skamarock, W.C., Klemp, J.B., (2008), A time-split nonhydrostatic atmospheric model for weather research and forecasting applications, Journal of Computational Physics, 227, p3465-3485.
[https://doi.org/10.1016/j.jcp.2007.01.037]

- USEPA (United States Environmental Protection Agency), (2003), Guidelines for Developing an Air Quality (Ozone and PM2.5) Forecasting Program, Research Triangle Park, NC.
-
Wang, Z.F., Li, J., Wang, Z., Yang, W.Y., Tang, X., Ge, B.Z., Yan, P.Z., Zhu, L.L., Chen, X.S., Chen, H.S., Wang, W., Li, J.J., Liu, B., Wang, X.Y., Wang, W., Zhao, Y.L., Lu, N., Su, D.B., (2014), Modeling study of regional severe hazes over Mid-eastern China in January 2013 and its implications on pollution prevention and control, Science China Earth Sciences, 57, p3-13.
[https://doi.org/10.1007/s11430-013-4793-0]

-
Zhang, Q., Streets, D.G., Carmichael, G.R., He, K.B., Huo, H., Kannari, A., Klimont, Z., Park, I.S., Reddy, S., Fu, J.S., Chen, D., Duan, L., Lei, Y., Wang, L.T., Yao, Z.L., (2009), Asian emissions in 2006 for the NASA INTEX-B mission, Atmospheric Chemistry and Physics, 9, p5131-5153.
[https://doi.org/10.5194/acpd-9-4081-2009]

-
Zhang, J.K., Sun, Y., Liu, Z.R., Ji, D.S., Hu, B., Liu, Q., Wang, Y.S., (2014), Characterization of submicron aerosols during a month of serious pollution in Beijing, 2013, Atmospheric Chemistry and Physics, 14, p2887-2903.
[https://doi.org/10.5194/acp-14-2887-2014]