Effect of Double Noise-Barrier on Air Pollution Dispersion around Road, Using CFD
Abstract
Noise-barriers on both sides of the roadway (hereafter referred to as double noise-barriers), are a common feature along roads in Korea, and these are expected to have important effects on the near-road air pollution dispersion of vehicle emissions. This study evaluated the double noise-barrier impact on near-road air pollution dispersion, using a FLUENT computational fluid dynamics (CFD) model. The realizable k-ε model in FLUENT CFD code was used to simulate vehicle air pollutant dispersion, in around 11 cases of double noise-barriers. The simulated concentration profiles and surface concentrations under no barrier cases were compared with the experimental results. The results of the simulated flows show the following three regimes in this study: isolated roughness (H/W=0.05), wake interface (H/W=0.1), and skimming flow (H/W> 0.15). The results also show that the normalized average concentrations at surface (z=1 m) between the barriers increase with increasing double noisebarrier height; however, normalized average concentrations at the top position between the barriers decrease with increasing barrier height. It was found that the double noise-barrier decreases normalized average concentrations of leeward positions, ranging from 0.8 (H/W=0.1, wake interface) to 0.1 (H/W =0.5, skimming flow) times lower than that of the no barrier case, at 10 x/h downwind position; and ranging from 1.0 (H/W=0.1) to 0.4 (H/W=0.5) times lower than that of the no barrier case, at 60 x/h downwind position.
Keywords:
CFD model, Double noise-barrier, Vehicle pollution dispersion, Inner barrier concentration retention, Concentration dilution behind barrier1. INTRODUCTION
Public health concerns related to near-road air quality have become a pressing issue, due to the increasing number of epidemiological studies suggesting that populations spending significant amounts of time near heavily trafficked roads are at a greater risk of adverse health effects (HEI, 2010). These effects may be attributed to increased exposure to the air pollutants emitted by vehicular traffic. The significant effect of vehicle emissions on urban populations worldwide has motivated research on methods to reduce exposure to these pollutants. Although emission control techniques and programs to directly reduce emitted air pollutants are essential components of air quality management, other options, including the preservation and planting of vegetation, and the construction of roadside structures, such as noise-barriers, may be near-term mitigation strategies that are useful for urban developers. These methods, if successful, can complement existing pollution control programs, or provide measures to reduce impacts from sources that are difficult to mitigate (Brantley et al., 2013).
The use of roadside barriers to mitigate near-road air quality is an attractive concept, given significant challenges associated with other means of reducing near-road air pollution in a timely manner (Hagler et al., 2011). Roadway design is being considered as one of the potential options. In particular, it has been suggested that noise-barriers, erected to reduce noise, may prove effectively at decreasing pollutant concentrations. However, there is still little information of how solid barriers affect pollutant transport, especially under a variety of barrier height and configuration conditions (Steffens et al., 2013).
Despite recent studies employing modeling, wind tunnel, and field measurements to evaluate the role of solid barriers on pollutant concentrations around road areas (Steffens et al., 2013; Hagler et al., 2011; Finn et al., 2010; Heist et al., 2009; Baldauf et al., 2008; Bowker et al., 2007), the extent to which double noise-barriers can reduce air pollution near roads, under varying noise-barrier heights, remains uncertain.
The dispersion of air pollution in complex situations, such as the case of noise-barriers in close proximity, is a difficult problem. Computational fluid dynamics (CFD) provides a method to build and run models that can simulate air pollution in such geometrically complex situations (Riddle et al., 2004). In this study, we utilized the Computational Fluid Dynamic model (FLUENT, 2006), to simulate the flow, and the concentrations, around double noise-barriers.
2. MATERIALS AND METHODS
2. 1 FLUENT CFD Software
FLUENT CFD software version 6.3.2 (FLUENT, 2006) was used to simulate wind flow and pollutant concentration around double noise-barriers. The simulations are based on Reynolds-averaged Navier-Stokes equations (RANS), using realizable k-ε. Four types of equations are solved in each case: the continuity equation (1), RANS equations (2), and two turbulence closure equations (4)-(5) for realizable k-ε, for the turbulent kinetic energy (k), and for the dissipation rate of turbulent kinetic energy (ε).
The continuity equation of incompressible fluid and the Reynolds-averaged Navier-Stokes equations are written as follows:
| (1) |
| (2) |
where, uj is the jth component of velocity, t is the time, xj is the jth coordinate, ρ is the air density, μ is the dynamic viscosity, and g is the gravitational body force.
| (3) |
Equation (3) is the Reynolds stress equation, where, is the turbulent viscosity. The governing equations of the realizable k-ε turbulence model are
| (4) |
| (5) |
where, , , and . In these equations, Gk represents the generation of turbulence kinetic energy due to the mean velocity gradients, Gb is the generation of turbulence kinetic energy due to buoyancy, and YM represents the contribution of the fluctuating dilatation in compressible turbulence, to the overall dissipation rate. The model constants are σk (=1.0), σε (=1.2), C1ε (=1.44), C2(=1.9). The degree to which ε is affected by the buoyancy is determined by the constant . Where v is component of the flow velocity parallel to the gravitational vector and u is the component of the flow velocity perpendicular to the gravitational vector (FLUENT, 2006). The pollutant dispersion patterns were analyzed, after solving the species transport equation, in conjunction with the turbulence model equations. The advection-diffusion (AD) module was applied to study the species transport process, by analyzing the mass fraction of pollutants in the mixture. FLUENT analyzes the mass diffusion process, based on the following equations (Ng and Chaw, 2014; Riddle et al., 2004):
| (6) |
where, Ji is the diffusion flux of the mixture (kg/m2s), ρ is the density of the mixture (kg/m3), Di is the mass diffusion coefficient of the pollutant in the mixture (m2/s), yi is the mass fraction of the pollutant (kg/kg), and μt is the turbulent viscosity (kg∙s/m). Similar to the other studies (Di Sabatino et al., 2007; Riddle et al., 2004), the turbulent Schmidt number was Sct specified as 0.7.
2. 2 Computational Domain and Boundary Conditions
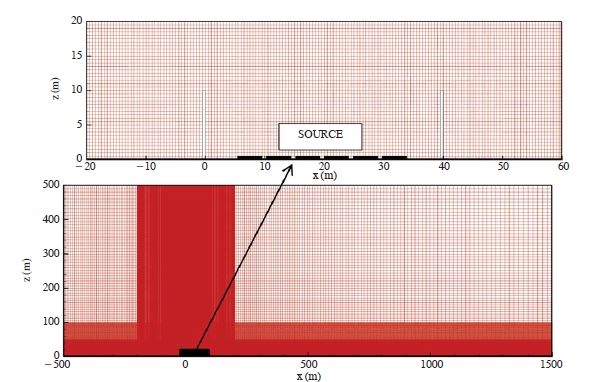
Fig. 1 shows a schematic diagram of the computational domain and mesh used to simulate the double noise-barriers. The atmospheric boundary layer considered in this study was a neutral boundary condition. The simulation was performed on a 2-dimensional domain, of 2,000 m length, and 500 m height. The model has a graduated mesh, ranging from 0.5 m in close proximity to the noise-barrier, and increasing with distance from the barrier, to 10 m maximum. The CFD modeling of 11 different double noise-barriers was performed, to study the flow fields, and the concentration distributions, resulting from emissions from a simulated six-lane highway. The width of the road (W) was fixed at 40 m, and the height of double noise-barriers (H) were 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, and 20 m, respectively. To simulate the traffic emission along a six-lane highway, six 4.5 m wide sources were installed in the simulation domain (Fig. 1).
The horizontal inhomogeneity of the wind flow profiles can result in unanticipated errors, which can be particularly significant for pedestrian-level wind conditions (Gorle et al., 2009; Yang et al., 2009; Richards and Hoxey, 1993). Richards and Hoxey (1993) proposed inflow boundary conditions of mean wind speed and turbulence quantities for the standard k-ε model that satisfied the transport equations for k and ε. This type of boundary conditions has been widely used in CWE (Computational Wind Engineering), based on the RANS method. Recently, Yang et al. (2009) derived the solution of the k equation of the standard k-ε model, and proposed a new set of inflow turbulence boundary conditions. The inlet boundary condition for U in the neutral boundary condition is:
| (6) |
where, u* is the frictional velocity; k is the von Karman constant; z0 has been introduced as a dimensional constant of integration and is commonly referred to as a roughness parameter or roughness length; and z is the height from surface. According to Gorle et al. (2009), if equilibrium between turbulence dissipation and production is imposed, the profile for k and ε has the following form.
| (7) |
where, A and B are constants that can be determined by fitting the equations to the measured profiles of k. Using the wind tunnel experimental results of Heist et al. (2009), for the profile under consideration, A= -0.075 and B=0.478 were selected in this study. The profile of ε is given by;
| (8) |
When using a commercial CFD code, however, the wall boundary condition is usually not as prescribed above. Blocken et al. (2007) provide a solution for this, by deriving a relationship that brings the rough wall functions into equilibrium with the inlet profiles. For FLUENT, this relation is given by:
| (9) |
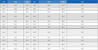
where, ks is the roughness height, and Cs is a constant required for the wall function. The roughness height should be smaller than the height of the center point of the wall adjacent cell, and was consequently set to 0.24 m. The resulting value for Cs is 1.428, defined through a User Defined Function. Table 1 lists the boundary conditions used in this study.
3. RESULTS AND DISCUSSION
3. 1 Evaluation of CFD Model Performance
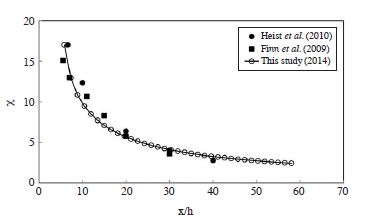
To evaluate the performance of the FLUENT model, Figs. 2 to 3 show the concentration profiles of the modeling and experimental results. In these figures, the data for Heist et al. (2009) are wind tunnel results, and the data for Finn et al. (2010) are field study results.
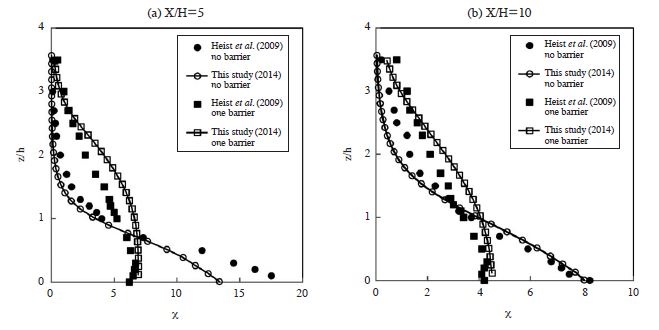
Comparison of experimental with CFD concentration profiles of no and one barrier cases at (a) x/h=5, (b) x/h=10.
The concentrations were normalized, to give the nondimensional concentration X=CUrLxLy/Q (Heist et al., 2009), where C is the concentration (a fraction by mass) with background concentration subtracted, Ur is the reference wind speed (equal to 12 m/s, measured at a full-scale equivalent height of 500 m), Q is the mass flow rate (0.01 kg/s of carbon monoxide), Lx is along the wind dimension of the roadway segment (30 m), and Ly is the lateral length of the source segment (because the simulation was conducted in a 2-dimensional domain in this study, Lx=1 was used). The length scale (x/h) was normalized with the height of the barrier (h=5 m). Fig. 2 shows the concentration profile of the no and one barrier (which is located at x=0m and the height is 6 m) cases, at x/h=5 and 10. The overall results show reasonable agreement with the experimental results, except that the simulated surface concentration profile at x/h=5 is about 20% smaller than that of the wind tunnel result. Fig. 3 shows a comparison between the calculated and experimental results of surface concentrations at z=1 m height. There is good agreement between the experimental data, and the CFD simulated results for a similar configuration.
3. 2 The Effect of Double Noise-barrier Height on Flow and Pollutant Concentration
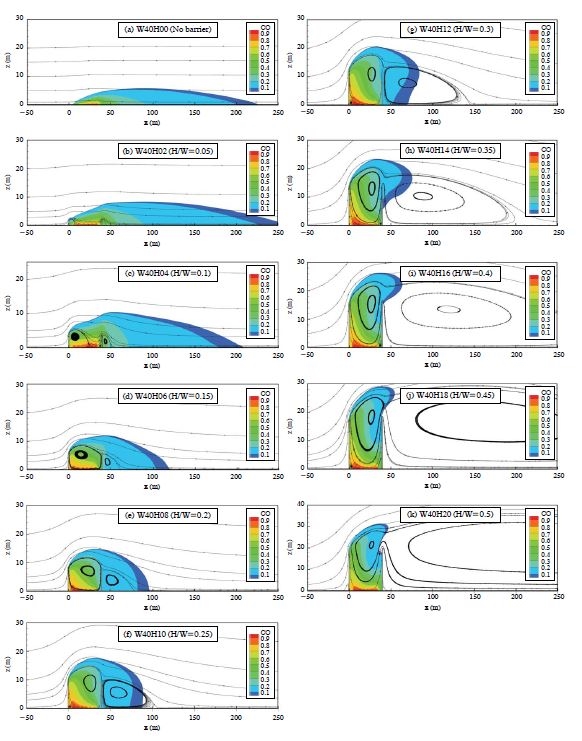
Fig. 4 shows the modeling results of 11 episode cases, with fixed road width, but changed barrier height, including the no barrier case. In these figures, the represented minimum mass fraction of carbon monoxide is 0.01.
Oke (1988) found that the characteristics of recirculation in a 2D idealized street canyon are determined by the building height-to-street-width aspect ratio H/W. The flows are divided into the following three regimes: isolated roughness (H/W<0.3), wake interface (0.3<H/W<0.65), and skimming flow (0.65<H/W). Analogously, a wind tunnel test was performed by Chang and Meroney (2003), and found that the skimming flow (H/W=1), wake interface (H/W=0.25), and isolated roughness (H/W=0.167) were also observed in 3D urban street canyons (Liu et al., 2011). It was supposed that the flow regime between the double noise-barriers is similar to that of the street canyon, with Fig. 4 representing the flow regime between the double noise-barriers. As shown in Fig. 4, isolated roughness (H/W=0.05, Fig. 4(b)), wake interface (H/W=0.1, Fig. 4(c)), and skimming flow (H/W>0.15, Figs. 4(d)-(k)) were observed in this study.
Concentration contours (Fig. 4) for different barrier heights reveal that the double noise-barrier height changes the vertical location of maximum concentration, downwind of a road. The presence of a double noisebarrier leads to a vertical lofting of emissions (Figs. 4(b)-(k)), with an increasing vertical velocity component, and lofting streamline on the roadway side of the wall with increasing barrier height. The mixing wake zone forms downwind from the noise-barriers. This mixing zone extends vertically up to, or slightly exceeds the barrier height, and extends horizontally approximately 2.5H (5.0 m) for the H=2m barrier, and 27H (540 m) for the H=20 m barrier. The vertical lofting of on-road emissions leads to reduced concentrations at the far field ground level, relative to the nobarrier case. In near-road field studies, the air pollution impact from major roadways is commonly detected at distances of several hundred meters (Hagler et al., 2011; Hu et al., 2009). So in general, the simulated results of this study are in line with those of other studies.
To show the concentration retention of double noise-barriers, normalized concentrations between the double noise-barriers (horizontal distances are from 0 to 40 m) at z=1m height are shown in Fig. 5. Normalized surface concentrations between the barriers show larger than that of the no barrier case (dashed line of Fig. 5). These increases of normalized concentrations increase with the increases of the noise-barrier height; however, normalized concentrations of the barrier top position show smaller, than that of the surface position (z=1 m).
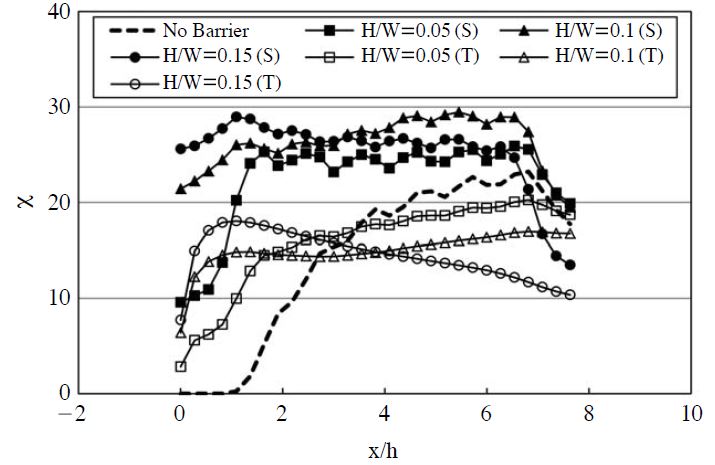
Normalized average concentrations of inner noisebarrier at z=1m and barrier top height (where S is surface and T is top).
Fig. 6 shows average normalized concentration at the surface, and top position between the barriers. The average normalized concentration was calculated, using 29 normalized concentration data between double noise-barriers. Normalized average concentrations at the surface increase with increasing barrier height, but normalized average concentrations at the top position decrease with increasing barrier height. Increasing normalized average concentrations at the surface and at the top, with the increasing of the noise-barrier height, was found in isolated roughness. Increasing normalized average concentrations at the surface and decreasing normalized average concentrations at the top, with the increasing of the noise-barrier height, was found in skimming flow.
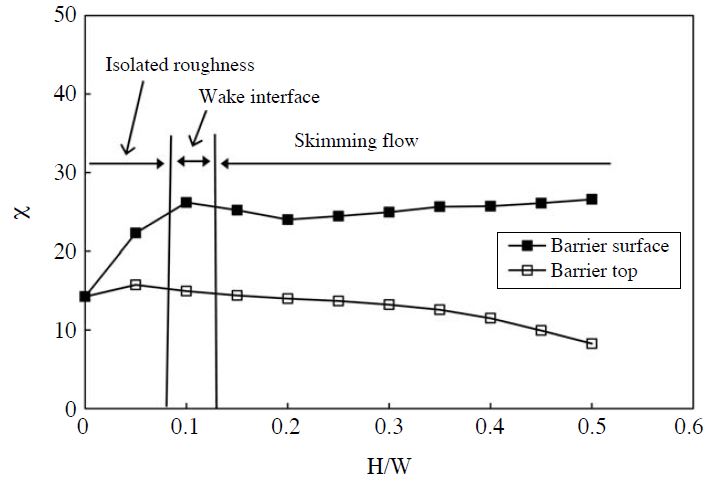
Flow regime and normalized average concentrations of barrier surface (z=1 m) and barrier top (from 2 to 20 m) of inner region of double-noise barriers.
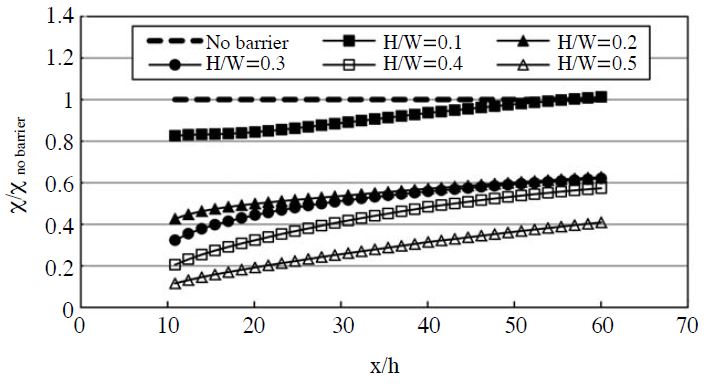
Fig. 7 shows normalized concentration leeward, behind the barriers. The reduction of near-road air pollution generally agrees with past findings, determining lower concentrations behind barriers. The overall normalized average concentrations of the windward position decrease, with increasing barrier height. The normalized average concentrations of leeward position show ranging from 0.8 (H/W=0.1, wake interface) to 0.1 (H/W=0.5, skimming flow) times lower, than that of the no barrier case, at 10 x/h downwind position; and ranging from 1.0 (H/W=0.1) to 0.4 (H/W =0.5) times lower, than that of the no barrier case, at 60 x/h downwind position.
4. CONCLUSIONS
This study utilized the Computational Fluid Dynamic model, to simulate the flow and concentrations around double noise-barriers. The realizable k-ε model in FLUENT CFD code was used to simulate the vehicle air pollutant dispersion, around eleven cases of double noise-barrier. The simulated no barrier results were compared with the experimental results.
The results revealed that the flows between the barriers in this study showed the following three regimes: isolated roughness (H/W=0.05), wake interface (H/W =0.1), and skimming flow (H/W>0.15). The results also show that normalized surface concentrations between the barriers show larger than those of the no barrier case. Normalized concentrations of the top position between the barriers show smaller, than that of surface positions (z=1 m). The double noise-barrier decreased normalized average concentrations of leeward position show ranging from 0.8(H/W=0.1, wake interface) to 0.1 (H/W=0.5, skimming flow) times lower, than that of the no barrier case, at 10 x/h downwind position; and ranging from 1.0 (H/W=0.1) to 0.4 (H/W =0.5) times lower, than that of the no barrier case, at 60 x/h downwind position.
Acknowledgments
This work was supported by Kyonggi University Research Grant 2013.
References
-
Baldauf, R., Thoma, E., Khlystov, A., Isakov, V., Bowker, G., Long, T., Snow, R., (2008), Impacts of noise barriers on near-road air quality, Atmospheric Environment, 42, p7502-7507.
[https://doi.org/10.1016/j.atmosenv.2008.05.051]

-
Blocken, B., Stathopoulos, T., Carmeliet, J., (2007), CFD simulation of the atmospheric boundary layer: wall function problems, Atmospheric Environment, 41, p238-252.
[https://doi.org/10.1016/j.atmosenv.2006.08.019]

-
Bowker, G.E., Baldauf, R., Isakov, V., Khlystov, A., Petersen, W., (2007), The effects of roadside structures on the transport and dispersion of ultrafine particles from highways, Atmospheric Environment, 41, p8128-8139.
[https://doi.org/10.1016/j.atmosenv.2007.06.064]

- Brantley, H.L., Hagler, G.S.W., Deshmukh, P.J., Baldauf, R.W., (2014), Field assessment of the effects of roadside vegetation on near-road black carbon and particulate matter, Science of the Total Environment, p468-469, 120-129.
-
Chang, C.-H., Meroney, R.N., (2003), Concentration and flow distributions in urban street canyons: wind tunnel and computational data, Journal of Wind Engineering and Industrial Aerodynamics, 91, p1141-1154.
[https://doi.org/10.1016/s0167-6105(03)00056-4]

-
Finn, D., Clawson, K.L., Carter, R.G., Rich, J.D., Eckman, R.M., Perry, S.G., Isakov, V., Heist, D.K., (2010), Tracer studies to characterize the effects of roadside noise barriers on near-road pollutant dispersion under varying atmospheric stability conditions, Atmospheric Environment, 44, p204-214.
[https://doi.org/10.1016/j.atmosenv.2009.10.012]

- FLUENT ver.6.3, (2006), User’s Guide.
- Gorle, C., Beeck, J., Rambaud, P., Tendeloo, G.V., (2009), CFD modelling of small particle dispersion: The influence of the turbulence kinetic energy in the atmospheric boundary layer, Atmospheric Environment, 43, p673-681.
-
Hagler, G.S.W., Tang, W., Freeman, M.J., Heist, D.K., Perry, S.G., Vette, A.F., (2011), Model evaluation of roadside barrier impact on near-road air pollution, Atmospheric Environment, 45, p2522-2530.
[https://doi.org/10.1016/j.atmosenv.2011.02.030]

- HEI, (2010), Traffic-related air pollution: a critical review of the literature on emissions, exposure, and health effects, HEI special report 17, Boston, MA, Health Effects Institute.
-
Heist, D.K., Perry, S.G., Brixey, L.A., (2009), A wind tunnel study of the effect of roadway configurations on the dispersion of traffic-related pollution, Atmospheric Environment, 43, p5101-5111.
[https://doi.org/10.1016/j.atmosenv.2009.06.034]

-
Hu, S.S., Fruin, S., Kozawa, K., Mara, S., Paulson, S.E., Winer, A.M., (2009), A wide area of air pollutant impact downwind of a freeway during pre-sunrise hours, Atmospheric Environment, 43, p2541-2549.
[https://doi.org/10.1016/j.atmosenv.2009.02.033]

-
Liu, C.H., Cheng, W.C., Leung, T.C.Y., Leung, D.Y.C., (2011), On the mechanism of air-pollutant re-entrainment in two dimensional idealized street canyons, Atmospheric Environment, 45, p4763-4769.
[https://doi.org/10.1016/j.atmosenv.2010.03.015]

- Ng, W.Y., Chau, C.K., (2014), A modeling investigation of the impact of street and building configurations on personal air pollutant exposure in isolated deep urban canyons, Science of the Total Environment, p468-469, 429-448.
-
Oke, T.R., (1988), Street design and urban canopy layer climate, Energy Bldg., 11, p103-113.
[https://doi.org/10.1016/0378-7788(88)90026-6]

- Richards, P.J., Hoxey, R.P., (1993), Appropriate boundary conditions for computational wind engineering models using the k-e model, Journal of Wind Engineering and Industrial Aerodynamics, 46&47, p145-153.
-
Riddle, A., Carruthers, D., Sharpe, A., Stocker, C.M.J., (2004), Comparisons between FLUENT and ADMS for atmospheric dispersion modeling, Atmospheric Environment, 38, p1029-1038.
[https://doi.org/10.1016/j.atmosenv.2003.10.052]

- Sabatino, S.D., Buccolieri, R., Pulvirenti, B., Britter, R., (2007), Simulations of pollutant dispersion within idealized urban-type geometries with CFD and integral models, Atmospheric Environment, 41, p8316-8329.
-
Steffens, J.T., Heist, D.K., Perry, S.G., Zhang, K.M., (2013), Modeling the effects of a solid barrier on pollutant dispersion under various atmospheric stability conditions, Atmospheric Environment, 69, p76-85.
[https://doi.org/10.1016/j.atmosenv.2012.11.051]

-
Yang, Y., Gu, M., Chen, S., Jin, X., (2009), New inflow boundary conditions for modelling the neutral equilibrium atmospheric boundary layer in computational wind engineering, Journal of Wind Engineering and Industrial Aerodynamics, 97(2), p88-95.
[https://doi.org/10.1016/j.jweia.2008.12.001]