A Methodological Comparison on Spatiotemporal Prediction of Criteria Air Pollutants
Copyright © 2022 by Asian Association for Atmospheric Environment
This is an open-access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0/), which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Air pollution monitoring devices are widely used to quantify at-site air pollution. However, such monitoring sites represent pollution of a limited area, and installing multiple devices for a vast area is costly. This limitation of unavailability of data at non-monitoring sites has necessitated the Spatio-temporal analysis of air pollution and its prediction. Few commonly used methods for Spatio-temporal prediction of pollutants include - ‘Averaging’; ‘Best correlation coefficient method’; ‘Inverse distance weighting method’ and ‘Grid interpolation method.’ Apart from these conventional methods, a new methodology, ‘Weighted average method,’ is proposed and compared for air pollution prediction at non-monitoring sites. The weights in this method are calculated based on both on the distance and directional basis. To compare the proposed method with the existing ones, the air pollution levels of NO2 (Nitrogen dioxide), O3 (Ozone), PM10 (Particulate matter of 10 microns or smaller), PM2.5 (Particulate matter of 2.5 microns or smaller), and SO2 (Sulphur dioxide) were predicted at the non-monitoring site (test stations) by utilizing the available data at monitoring sites in Delhi, India. Preliminary correlation analysis showed that NO2, PM2.5, and SO2 have a directional dependency between different stations. The ‘average’ method performed best with the mode RMSE of 18.85 μg/m3 and R2 value 0.7454 when compared with all the methods. The RMSE value of the new proposed method ‘weighted average method’ was 21.25 μg/m3, resulting in the second-best prediction for the study area. The inverse distance weighting method and the Grid interpolation method were third and fourth, respectively, while the ‘best correlation coefficient’ was the worst with an RMSE value of 41.60 μg/m3. Results also showed that the methods that used dependent stations had performed better when compared to methods that used all station data.
Keywords:
Correlation, Prediction, Methodology comparison, Air pollutants, Correlation analysis, Delhi, Interpolation, Dependency, Spatiotemporal, Non monitoring station, Weighted average1. INTRODUCTION
Pollutants, the undesired substances, degrade the ecosystem with their adverse effects and cause pollution. When concerned with the imbalance in the atmosphere, this pollution is called air pollution. It kills an estimated seven million every year, with low- and middle-income countries suffering the most (Osseiron and Lindmeier, 2018; WHO, 2018). A significant relationship between atmospheric pollutants and health hazards is reported, and their exposure increases the risk of cardiovascular diseases, fertility issues, and mental health in particular (Chen et al., 2018; Manan et al., 2018; Merklinger-Gruchala et al., 2017; Curtis et al., 2006; Mortimer et al., 2002; Wong et al., 2001). Particulate matter variation studies in India have shown Delhi as the most polluted city when compared to Kolkata, Mumbai, Hyderabad (Singh et al., 2021), with values of PM2.5 (Particulate matter of 2.5 microns or smaller) and PM10 (Particulate matter of 10 microns or smaller) exceeds National Ambient Air Quality Standards (NAAQs) 60 mg/m3 (Guo et al., 2019). Studies have attributed agricultural fires as one of the reasons for this (Cusworth et al., 2018). Furthermore, the existence of the relationship between the outbreak of COVID-19 and air pollution is also reported (Roy, 2021). Moreover, an increase in levels of NO2 (Nitrogen dioxide), O3 (Ozone), and SO2 (Sulphur dioxide) have potential health concerns (WHO, 2018).
Considering the harmful nature of these pollutants, it is important to monitor these pollutants. However, due to the high cost of placing monitoring instruments everywhere, sometimes the pollutants can be predicted at a non-monitoring site using various available methods. There have been a number of studies around the globe that have predicted these criterion air pollutants using machine learning (Qi et al., 2019; Wen et al., 2019; Yeganeh et al., 2018; Fan et al., 2017; Zou et al., 2015; Papaleonidas and Iliadis, 2013; Rigol et al., 2001) and Regression models (Kerckhoffs et al., 2021; Boaz et al., 2019; Wang and Song, 2018; Alam and McNabola, 2015; Russo and Soares, 2014; Dominick et al., 2012; Crouse et al., 2009).
There have also been some studies, wherin a comparison of various methods to predict these pollutants have been done. The spatial interpolation methods such as geostatistical methods (various kriging methods), local interpolators (Thiessen polygons, IDW, splines), global interpolators (trend surfaces or regression models), and mixed methods were analyzed by Vicente-Serrano et al. (2003). Spatial interpolation methodologies were summarized for urban air pollution modeling based on the application for the greater area of metropolitan Athens, Greece (Deligiorgi and Philippopoulos, 2011). The proposed methodologies include Nearest neighbor method, Triangulated irregular network method, Natural neighbor method, Inverse distance weighting (IDW) method (with linear and squared IDW), Radial basis function (RBF) method, Thin plates splines method, Kriging method, and Artificial neural network (ANN) method. The application of spatial interpolation methods was given to many disciplines (Li and Heap, 2011). A total of 72 spatial interpolation methods were analyzed, and comparative performances were provided in their study by Li and Heap (2014). They included the most frequently used methods as Inverse distance weighting (IDW), ordinary kriging (OK), and ordinary co-kriging (OCK) also. The spatiotemporal prediction at the non-monitoring site was presented by Alimissis et al. (2018) using interpolation methods to determine the air pollution at a new location.
Some previous studies in India focused on the missing data prediction using previous data of pollutants or meteorological data or their combinations as predictors. Singh et al. (2012) provides a comparison of the linear (PLSR) and nonlinear (MPR, MLPN, RBFN, and GRNN) models for urban air quality prediction (RSPM, SO2, NO2) using data of temperature, relative humidity, wind speed, SPM, NO2, and SO2 data and shown more remarkable performances of GRNN models than the MLPN and RBFN. Nagendra and Khare (2006, 2005) compared among three choices of input data sets for the prediction of NO2 firstly, using meteorological and traffic data, secondly, using only meteorological data, and lastly using only traffic data. MLR and PCA+ANN models were evaluated with statistical analysis by Mishra and Goyal (2015) for NO2 forecasting models at Taj Mahal, Agra using NO2, SO2, temperature, CO, O3, RH, WS, and WDI (wind direction index) as predictors. The performances of PCA approaches were found better than the MLR in their analysis. The performance for the MLP model was found better as compared to RBF and GRNN models for all seasons (Kumar et al., 2017).
Thus, the prediction studies of air pollution have been done for a particular location to evaluate the missing data using the pollution data and meteorological data of that location or a combination of both. The studies have also been done to predict air pollution at a location using pollution data of other sites and other predictors. However, the studies predicting the air quality at a new location (other than monitoring site) using spatial interpolation methods have not been done in India.
In this study, the prediction of air quality parameters at a location of a non-monitoring site is presented over Delhi, India. The air pollution data of the neighboring monitoring sites have been used for the predictions of NO2, O3, PM10, PM2.5, and SO2. The specific objectives of the present study are:
- (i) Prediction of criteria air pollutants (NO2, O3, PM10, PM2.5, and SO2) at non-monitoring sites in Delhi using five different methods (average method, best correlation coefficient method, weighted average, inverse distance weighting method, and grid interpolation method).
- (ii) To compare the performance of these five methods on the basis of prediction efficiency.
2. STUDY AREA AND DATA USED
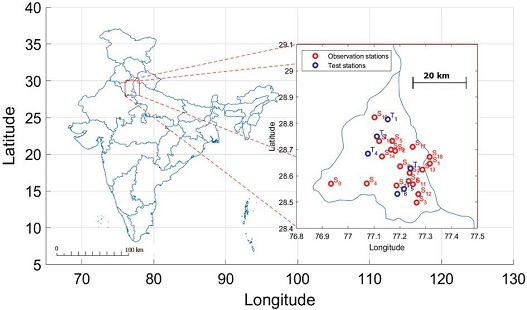
The present study is conducted for Delhi, India; located between 28.42°N to 29.00°N latitude and 76.86°E to 77.36°E longitude (Fig. 1). Delhi is one of the major cities in India, with rapid growth in population, traffic, industrialization and construction activities. This has led to higher energy consumption. Moreover, the availability of alternate energy sources is limited, thus further increasing the air pollution in Delhi. The air quality observation data for the study area is obtained from CPCB (Central Pollution Control Board of India) at ‘https://app.cpcbccr.com/AQI_India/’, and the same is also provided at ‘https://openaq.org/’. Table 1 shows the statistical summary of fifteen minutes scaled dataset of the five pollutants (PM2.5, PM10, NO2, SO2, and O3) for the 46 stations over Delhi in the period of January 1, 2018, to October 30, 2020.
Analysis showed that, only 25 of these stations had missing data less than 75%, which were used for prediction and validation. The top six monitoring stations (Table 2) having maximum missing data out of the 25-monitoring station was reserved for validation, while the remaining 19 monitoring station with the lowest missing percentage was used for prediction model development purposes (Table 3).
3. METHODOLOGY
In this study five different methods (Simple Averaging, Best Correlation Coefficient Method, Weighted Average Method, Inverse Distance Weighting method, and Grid Interpolation Method) have been evaluated in terms of prediction efficiency. Theses are the methods which are commonly used in the previous studies (Jin et al., 2011). The correlation analysis was performed to check the dependency among the chosen monitoring stations. The correlation analysis was performed between 19 monitoring stations using the entire data at 15 min intervals at seasonal (Winter: January and February), Summer: March, April, and May, Monsoon: June to September, and Post-monsoon period: October to December) and annual scales.
3. 1 Correlation Analyses
The correlation coefficients between all possible pairs of 19 observation monitoring stations were evaluated for each season and pollutant. The value of the correlation coefficient to be satisfactory depends on the purpose for which it is used and the nature of raw data. The broad classification of correlation coefficients for their correlation strength is given in Asuero et al. (2006). The pair of stations showing average or high correlation was treated to have a positive dependency. A linear model was established among the correlation coefficients between each pair as output variable, distances between two stations, and direction of the line joining the two stations as input variables.
| (1) |
where, r(Oi, Oj) is the correlation coefficient between the observation of the ith and jth observation monitoring stations.
If the spatial coordinates of the ith and jth observation monitoring stations are given as
- SOi = (lati, longi)
- SOj = (latj, longj)
then, d(SOi, SOj) is the linear distance between the ith and jth observation 156 whose mathematical expression given by
| (2) |
θ(SOi, SOj) is the direction of the line joining ith and jth observation monitoring stations, whose mathematical expression is given as
| (3) |
The constants C1, C2, and C3 are determined by multivariate 162 correlation coefficient, linear distance, and direction of the line joining 163 for each season and pollutants. Thus, the possible correlation coefficient 164 station and observation station for any pollutant can be evaluated 165 established linear model.
| (4) |
where, r(Ti, Oj) is the correlation coefficient, d(STi, SOj) is the linear distance, and θ(STi, SOj) is the direction of the line joining between ith test station and jth observation monitoring station.
3. 2 Prediction Methods
The model established in the correlation analysis was used to evaluate the dependency of pollutants concentration of observation stations (monitoring stations) on the test station pollutants concentration based on the spatial characteristic of the test station with respect to observation stations. The correlation coefficient was evaluated between test stations and observation stations for each pollutant using the established linear model (Equation 4).
This method gives the average value of the pollutant of nearby monitoring stations, which shows positive dependency (R>0.5) with the site to be predicted. It can be mathematically expressed as
| (5) |
where, C(STi, t0) is the pollutant concentration at ith test station on time t0, and C(SOj, t0) is the pollutant concentration at the jth dependent observation station on time t0.
The linear model was established among the correlation coefficients as output variable, distances between two stations, and direction of the line joining the two stations as input variables (Equation 4). Using this linear model, the correlation coefficients between the desired point location and available data point locations are predicted from the distances and directions.
This method states that the data point of the best correlation station with the desired location should be considered the predicted values for the desired location.
| (6) |
| (7) |
where, C(STi, t0) is the pollutant concentration at ith test station on time t0, C(SOk, t0) and is the pollutant concentration at kth dependent observation station having maximum correlation coefficient on time t0.
The correlation coefficient was evaluated between test stations and observation stations for each pollutant in each season using the established linear model (Equation 4). The pollutants concentrations were assumed to be linearly dependent on the nearby dependent observation stations.
| (8) |
| (9) |
| (10) |
| (11) |
where C(STi, t0) is the pollutant concentration at ith test station on time t0, and C(SOj, t0) is the pollutant concentration at the jth dependent observation station on time t0. Cf is the observation station data, and MD is its dependent station data matrix. B is the coefficients of proportionality between Cf and MD.
The coefficients of linearity (weights for each dependent observation station) for any observation station are assumed to be linearly dependent on the distance of the observation station and the direction of the line joining that observation station.
| (12) |
Now the coefficients B′ between test station and observation stations are back-calculated using K1 and K2.
| (13) |
Thus, in this method, mass concentration pollutants at test are given as a sum of multiplication of pollutants concentration data of dependent observation stations with their weights (proportionality coefficients determined earlier for each observation station).
| (14) |
The principle of this method is that the observation station having more distance from the test station will affect the least to test station and vice versa. In this method, the weights are distributed among the dependent observation stations according to their inverse distance from the test station. The dependency of the observation stations is determined from the correlation analysis (Equation 4). The generic equation for the Inverse Distance Weighting (IDW) method (Bartier and Keller, 1996) was given as
| (15) |
where C(STi, t0) is the pollutant concentration at ith test station on time t0, and C(SOj, t0) is the pollutant concentration at jth dependent observation station on time t0.
In this method, the grid interpolation (using the nearest neighbor method) has been done for query points (entire grid) over the scattered pollutants data by the fitting surface over the area. The mass concentration data obtained by interpolation at the query point (location at which the pollution concentrations are to be predicted) is considered the predicted data.
a. Grid interpolation with dependent station data
The observation stations dependent on the particular test station (R>0.5) were used as input data for interpolation in a specific season for a specific pollutant.
b. Grid interpolation with all station data
The data of all observation stations were used as input for the interpolation in a particular season for a specific pollutant.
4. RESULTS AND DISCUSSION
4. 1 Correlation Analyses
The performance analyses in this study were carried using the Root Mean Square Error (RMSE) and Correlation Coefficient (R2). Considering O and P as the observed and predicted concentrations, the formula for RMSE and R2 are as shown below:
| (16) |
| (17) |
The correlation plots between 19 observation stations for different pollutants are shown in Figs. 2(a) to (e). Lower value of correlation coefficient does not provide sufficient relation, hence, in this study a threshold value of 0.5 was considered. All values having correlation coefficient less than 0.5 were removed in this study. The color and width of the line represent the magnitude of the correlation between the two observation stations. The larger width and red color signifies higher correlation whereas, the smaller width and blue color represent a lower correlation.
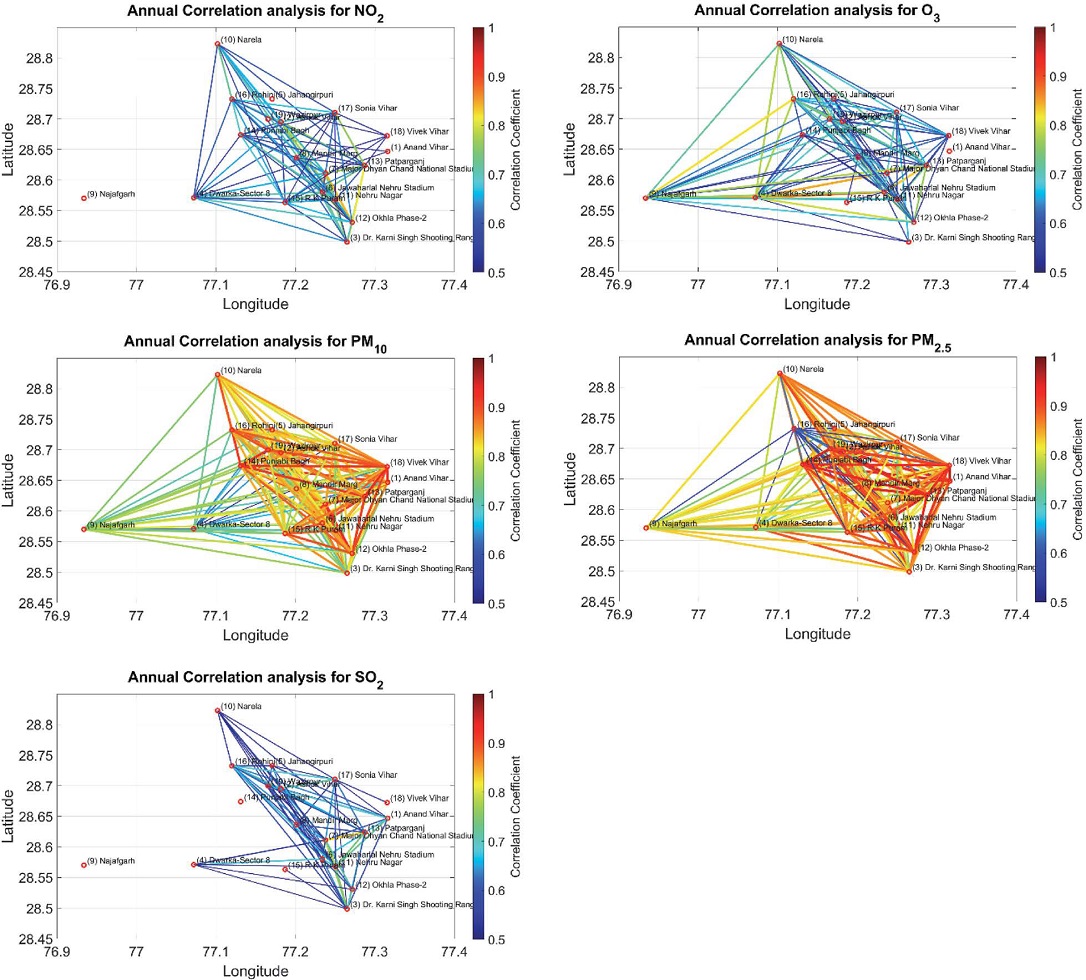
Spatial plot of observation stations showing the strength of correlation coefficient calculated on annual data over three years using colour and weight of the line for NO2, O3, PM10, PM2.5 and SO2.
It can be seen that the correlations are strongest for PM10 (Fig. 2(c)) and PM2.5 (Fig. 2(d)), whereas weakest for SO2 (Fig. 2(e)). However, a weak directional dependency was also observed for SO2 along the NW-SE direction, as the strength of the correlation is always lower in this direction.
The number of pairs of stations showing a good correlation with their frequency of occurrence along with five pollutants and five seasons is shown in the histogram (Fig. 3). Dwarka-Sector 8, Delhi - DPCC shows a good correlation in 24 out of 25 cases (for five pollutants along five seasons) with Jawaharlal Nehru Stadium, Delhi - DPCC always a good correlation with the Jawaharlal Nehru Stadium monitoring station. The monitoring station pairs having good correlation in 23 out of 25 cases are given in Table 4.
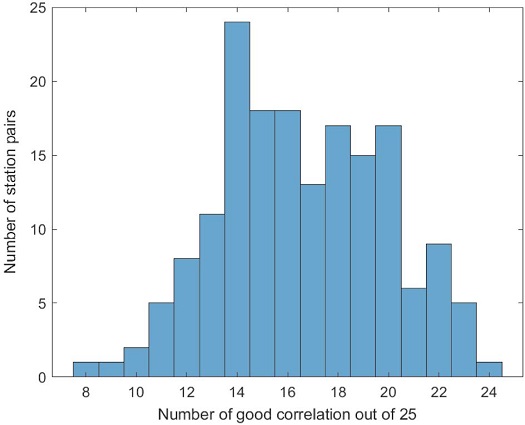
Histogram showing the frequency of the combination of observation station pairs with the number of times having good strength of correlation out of 25 cases (for five pollutants in 5 seasons).
4. 2 Prediction of Pollutant’s Concentration
The predictions of the pollutant’s concentration at 15 minutes intervals have been made for three years by five various methods in all seasons for five pollutants at six validation stations. For the purpose of inter-comparison between different pollutants, instead of RMSE, the PRMSE (Percentage RMSE) was used to prepare the box plots. These box plots were prepared both for 15-minute interval and daily averages.
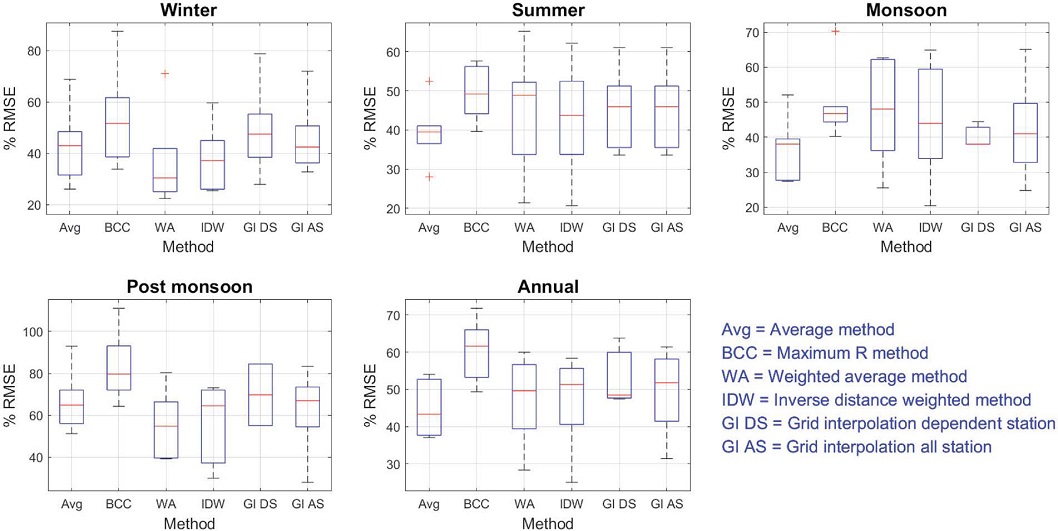
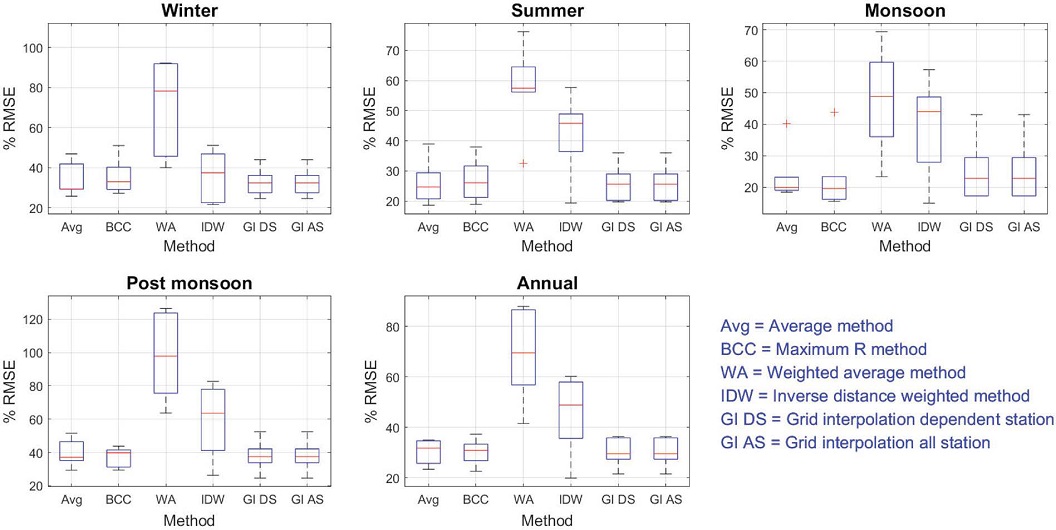
The box plots showing PRMSE for NO2 in different seasons and by different methods are shown in Fig. 4. Overall, the weighted-average prediction method shows the best performance having the lowest median PRMSE and least interquartile range for three seasons. However, on the annual scale, even the Average method shows better consistency and accuracy.
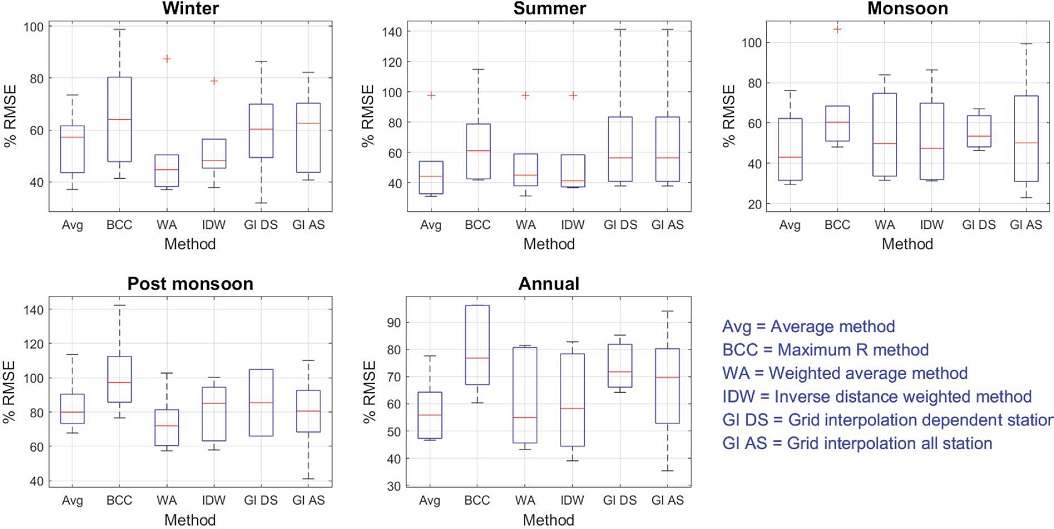
Box plot of PRMSE of predictions by various methods at six validation stations in various seasons for NO2.
Due to the conversion of the 15 minutes interval prediction data into daily data, the interquartile range and median RMSE have been reduced to 12.92 μg/m3 on average (Fig. 5). It can still be seen that the pattern of performance among the methods of prediction is similar to 15-minute interval case.
The presence of outliers shows the variations of predictions at different test stations are more in the summer season for the prediction of O3 (Figs. 6 and 7). All the methods of prediction have almost similar behavior for the prediction of O3. The missing box plot for any method shows the unpredictability of that method due to the lack of dependent observation station data (R>0.5) in the respective season.
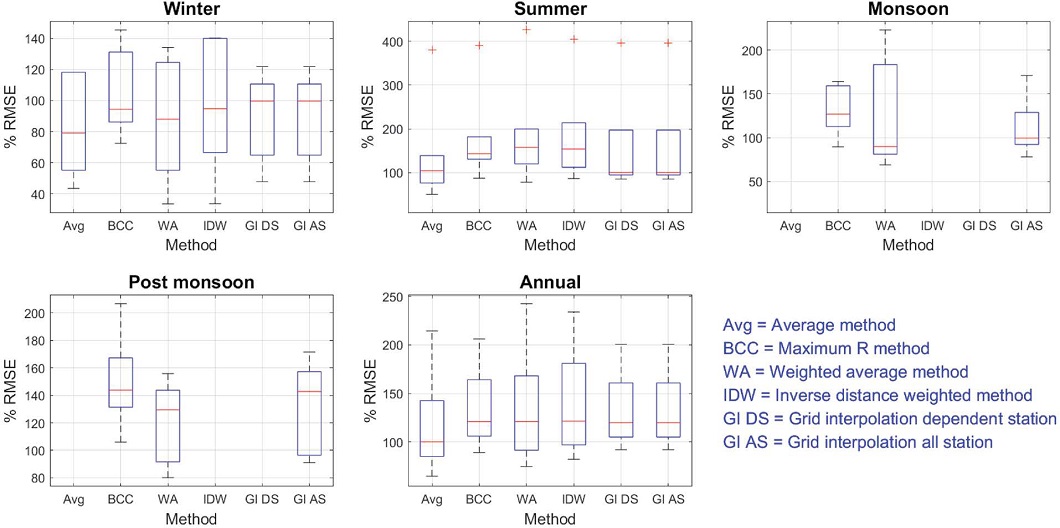
Box plot of PRMSE of predictions by various methods at six validation stations in various seasons for O3.
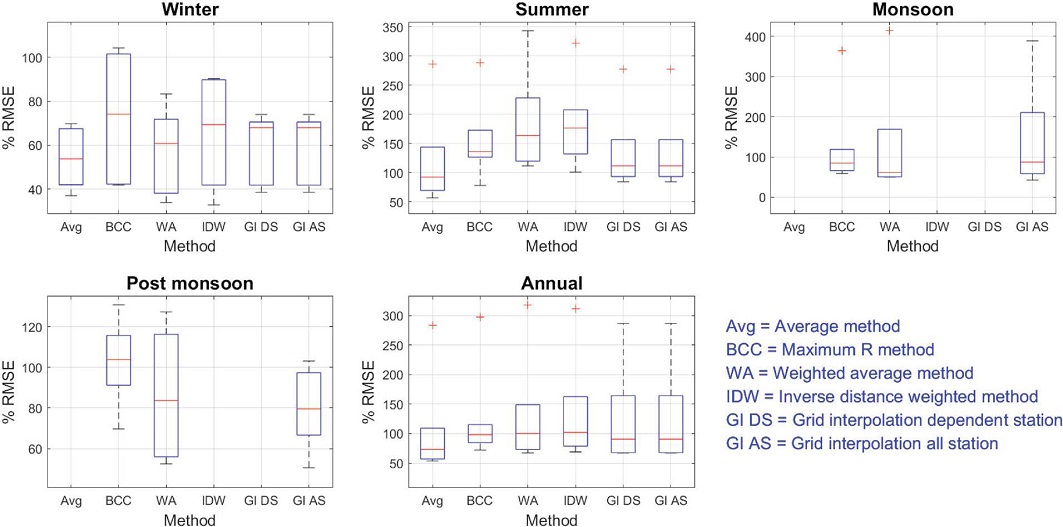
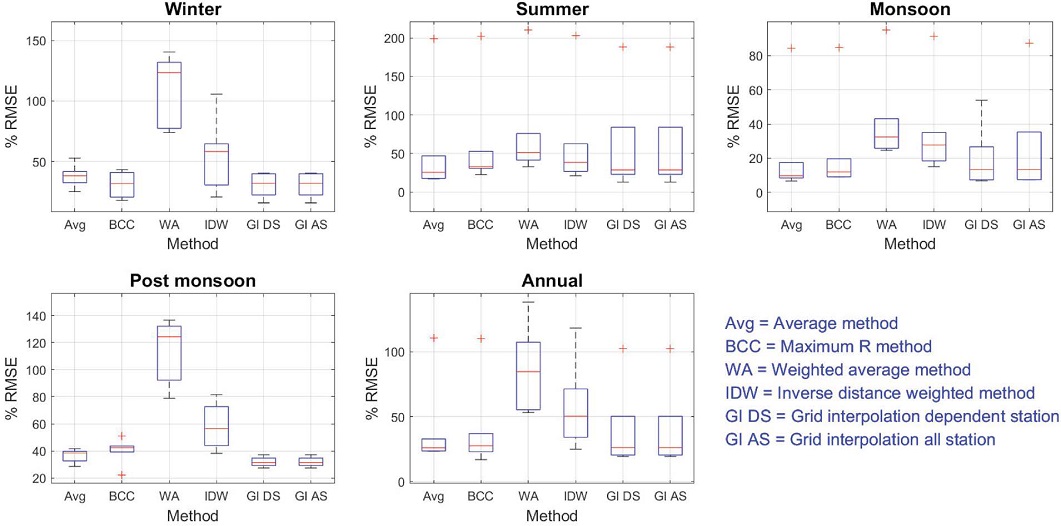
The RMSE of predictions is greater for PM10 than NO2 and O3. The weighted average method has worse prediction (highest median PRMSE and interquartile range in all seasons) than other methods (Figs. 8 and 9) in all seasons for the prediction of PM10.
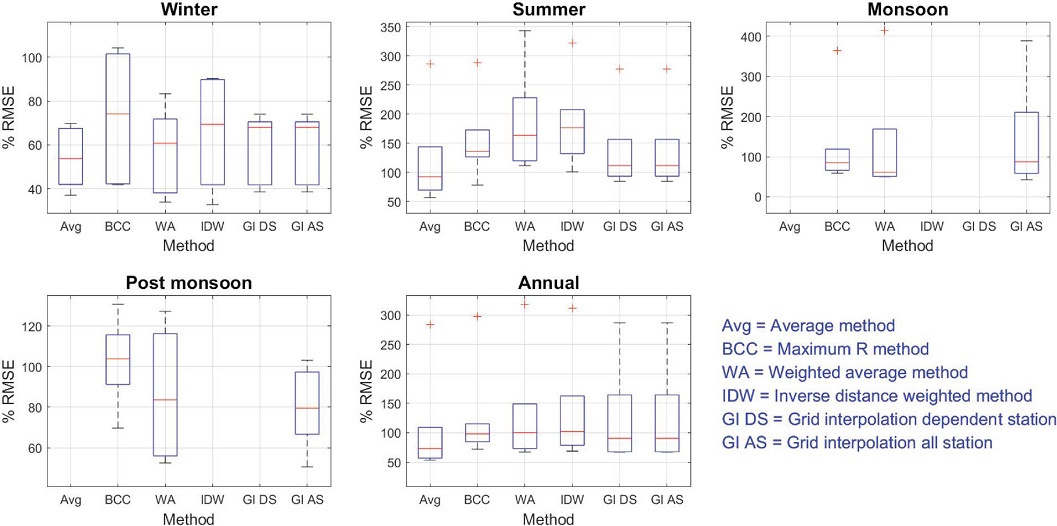
Box plot of PRMSE of predictions by various methods at six validation stations in various seasons for PM10.
The presence of outliers shows the more significant variations of predictions at different test stations in every season for the prediction of PM2.5 (Figs. 10 and 11). All the predictions methods have almost similar behaviour for the prediction of PM2.5 except the Weighted average method in some seasons (winter and post-monsoon). The prediction by the Weighted average method is the worst among all the methods for PM2.5 prediction.
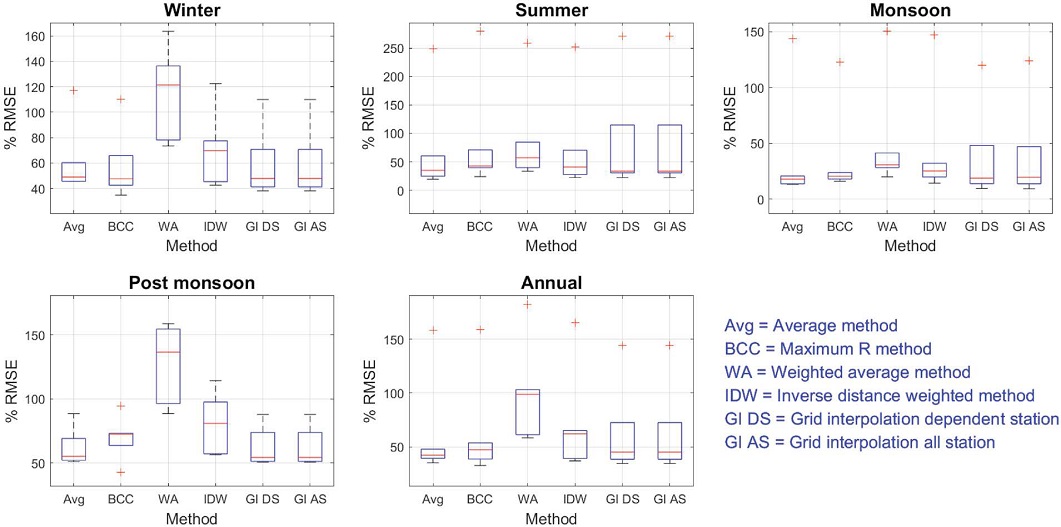
Box plot of PRMSE of predictions by various methods at six validation stations in various seasons for PM2.5.
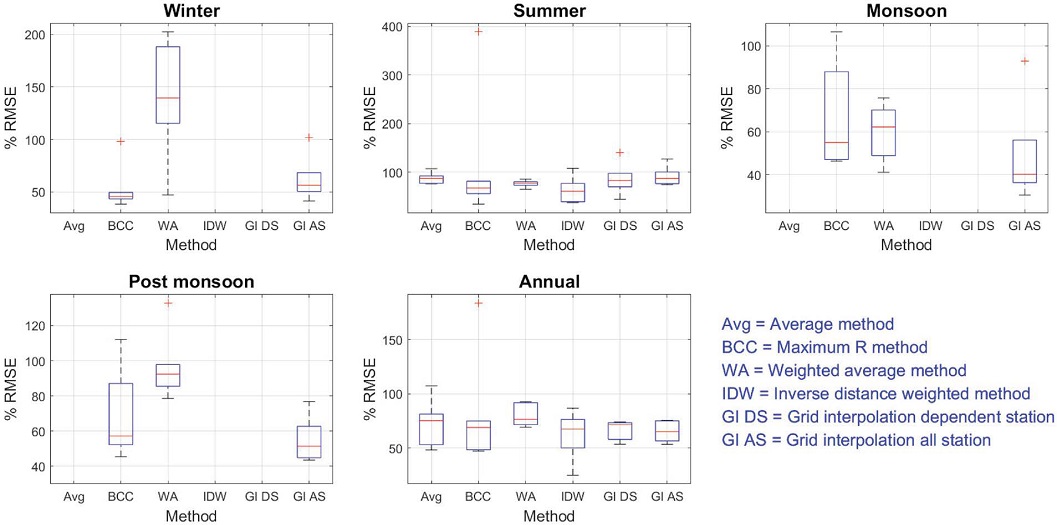
The missing box plot for any method shows the unpredictability of that method due to the lack of dependent observation station data in the respective season. All the methods of prediction have almost similar behaviour for the prediction of SO2 (Figs. 12 and 13).
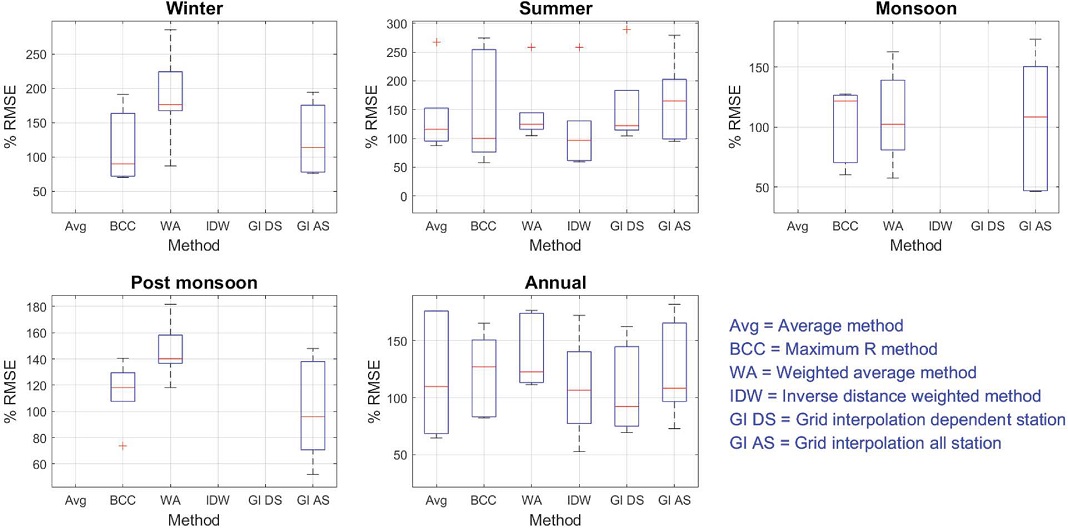
Box plot of PRMSE of predictions by various methods at six validation stations in various seasons for SO2.
4. 3 Performance of Methodologies
The RMSE and R2 of predictions were calculated for each prediction method in each season for each pollutant and at each test station. These RMSE and R2 were grouped for each methodology, and histogram plots were shown representing the frequencies of occurrence of RMSE with mode, median and average values.
The performance of the Average method was found to be having the best predictions most of the time with mode RMSE of 18.85 (Fig. 14), R2 of 0.74 (Fig. 15), and the performance of the Best correlation coefficient (BCC) method was found to be having the worst predictions most of the times with mode RMSE of 41.60 (Fig. 14). These results are similar to some of the previous studies (Alam et al., 2015: max R2=0.66; Crouse et al., 2009: max R2=0.8; Qi et al., 2019: max R2=0.72).
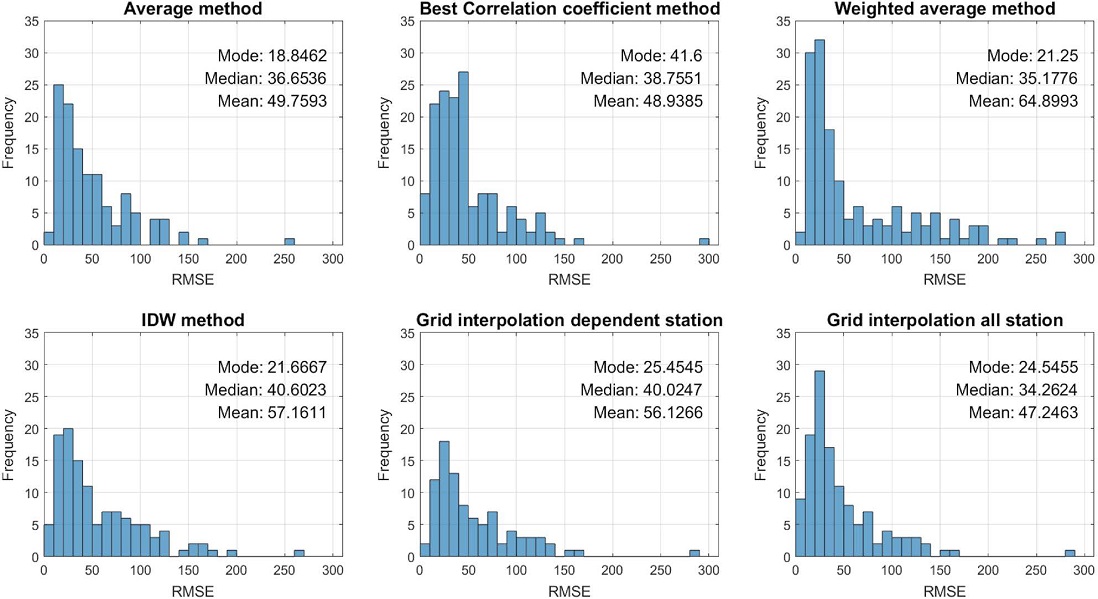
Histogram plot showing frequencies of RMSE over various pollutants, seasons, and test stations for each prediction method.
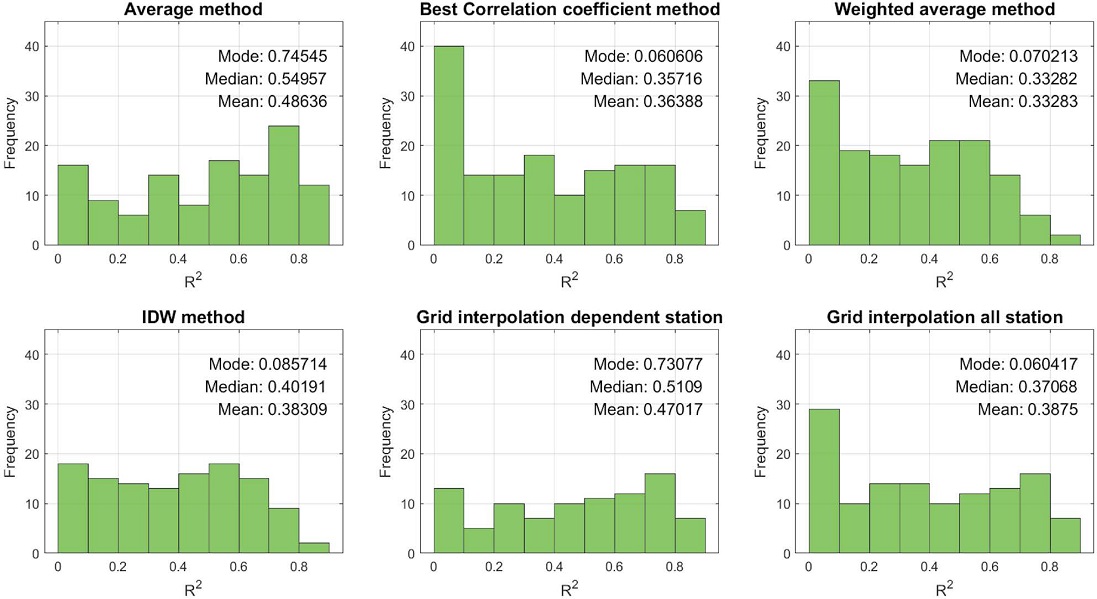
Histogram plot showing frequencies of R2 over various pollutants, seasons, and test stations for each prediction method.
The scatter plot of the prediction having least and maximum RMSE among all the combinations of prediction methods, seasons, and test stations have also been shown for each pollutant. The method showing the best performance for any of the stations/seasons is chosen, and the corresponding scatter plot is shown in Fig. 16(a)-(e).
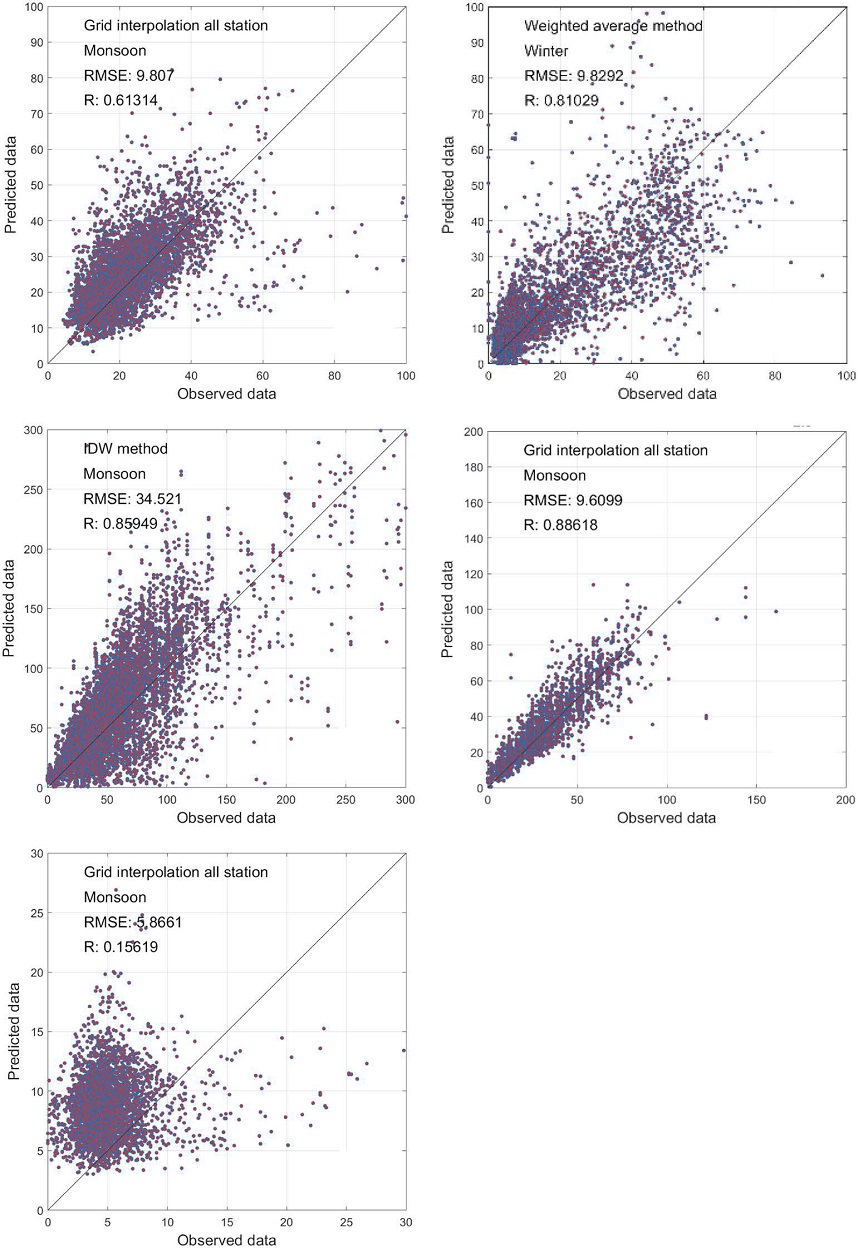
Scatter plot of the best prediction (having least RMSE) among all seasons, method of predictions, and test stations for (a) NO2, (b) O3, (c) PM10, (d) PM2.5, (e) SO2.
The least RMSE has been achieved to predict PM2.5 by Grid interpolation using all observation station data in monsoon season (Fig. 16(d)) with a high correlation coefficient of 0.88. In contrast, the least RMSE has been achieved to predict SO2 by Grid interpolation using all observation station data in monsoon season (Fig. 16(e)) with a very low correlation coefficient of 0.15.
Most of the time, the best predictions have been achieved in monsoon season and with the grid interpolation method at all stations.
5. SUMMARY
The increasing availability of historical data, the number of monitoring stations, and computing resources have facilitated us to develop more advanced models for air pollution prediction. In this study, a methodological comparison to predict the mass concentration of NO2, O3, PM10, PM2.5, and SO2 at any non-monitoring site was carried out.
A correlation analysis was done to check the interdependency of pollutants concentration data among the different observation stations. The correlation matrix was calculated based on the pollutant’s concentration data of three years. Further, a model is established based on the correlation coefficients between any pair, their distance, and the direction of the line joining among the 19 monitoring stations of Delhi. This model predicts the strength of correlation between non-monitoring sites and 19 monitoring stations of Delhi.
Five different methods were adopted to predict mass concentrations at non-monitoring sites using the mass concentration data of those monitoring sites, showing a good correlation with non-monitoring sites. Six additional monitoring stations’ mass concentrations data were used to validate predicted mass concentrations at those sites. The percentage errors and RMSE were calculated, and comparison was carried out among the methodologies in different seasons for each pollutant.
The correlation between the two monitoring stations has no relation with the direction of their spatial position (direction of the line joining them). The results showed that a simple average on the dependent station model performed best over other methods. The performance of the proposed method is also consistent both for optimal prediction at all stations and has the second minimum mode RMSE among different prediction methods. These methods can be used in future studies and other regions for air pollutant prediction.
6. CONCLUSIONS
The conclusions of the present study can be enumerated as:
- 1) Based on the correlation analysis, we found that the stations showed higher correlations for the Particulate matter (PM2.5 and PM10) compared to other pollutants.
- 2) Overall, the Grid interpolation method with dependent station was found the best (lowest median RMSE=5,107.5 μg/m3) whereas the Weighted Average was the worst (maximum RMSE=9,734.9 μg/m3).
- 3) Averaging is found to be the best prediction method based on mode RMSE(=18.85 μg/m3), whereas the Best correlation coefficient method was found to be the worst prediction method (mode RMSE 41.60 μg/m3).
- 4) Overall, the prediction for SO2 was the best among all the pollutants whereas for O3, it was the worst. Considering different seasons, it was easier to predict the pollutants in the monsoon season, whereas it was most difficult in the post monsoon season. This can be attributed to corresponding level of pollution in these seasons.
- 5) The methods that used dependent station data (Average, IDW, and GI DS) always have greater mode R2, whereas the methods that used all station data (BCC, WA, and GI AS) always have mode R2 smaller as 0.1 (Fig. 15).
7. LIMITATIONS
One of the major limitations of this study is the lack of available information about point source pollution. If emission data about these major point sources were available, proper weights could be assigned to these stations based on distance and direction from the source of pollution. Moreover, the distances between the stations is small, therefore the outcomes of the study may be limited only up to the spatial extent of the study area.
References
-
Alam, M.S., McNabola, A. (2015) Exploring the modeling of spatiotemporal variations in ambient air pollution within the land use regression framework: Estimation of PM10 concentrations on a daily basis. Journal of the Air & Waste Management Association, 65(5), 628-640.
[https://doi.org/10.1080/10962247.2015.1006377]

-
Alimissis, A., Philippopoulos, K., Tzanis, C.G., Deligiorgi, D. (2018) Spatial estimation of urban air pollution with the use of artificial neural network models. Atmospheric Environment, 191, 205-213.
[https://doi.org/10.1016/j.atmosenv.2018.07.058]

-
Asuero, A.G., Sayago, A., González, A.G. (2006) The correlation coefficient: An overview. Critical Reviews in Analytical Chemistry, 36(1), 41-59.
[https://doi.org/10.1080/10408340500526766]

-
Bartier, P.M., Keller, C.P. (1996) Multivariate interpolation to incorporate thematic surface data using inverse distance weighting (IDW). Computers and Geosciences, 22(7), 795-799.
[https://doi.org/10.1016/0098-3004(96)00021-0]

-
Boaz, R.M., Lawson, A.B., Pearce, J.L. (2019) Multivariate air pollution prediction modeling with partial missingness. Environmetrics, 30(7), e2592.
[https://doi.org/10.1002/env.2592]

-
Chen, S., Oliva, P., Zhang, P. (2018) Air Pollution and Mental Health: Evidence from China.
[https://doi.org/10.3386/w24686]

-
Crouse, D.L., Goldberg, M.S., Ross, N.A. (2009) A prediction-based approach to modelling temporal and spatial variability of traffic-related air pollution in Montreal, Canada. Atmospheric Environment, 43(32), 5075-5084.
[https://doi.org/10.1016/j.atmosenv.2009.06.040]

-
Curtis, L., Rea, W., Smith-Willis, P., Fenyves, E., Pan, Y. (2006) Adverse health effects of outdoor air pollutants. Environment International, 32(6), 815-830.
[https://doi.org/10.1016/j.envint.2006.03.012]

-
Cusworth, D.H., Mickley, L.J., Sulprizio, M.P., Liu, T., Marlier, M.E., Defries, R.S., Guttikunda, S.K., Gupta, P. (2018) Quantifying the influence of agricultural fires in northwest India on urban air pollution in Delhi, India. Environmental Research Letters, 13(4), 044018.
[https://doi.org/10.1088/1748-9326/aab303]

-
Deligiorgi, D., Philippopoulos, K. (2011) Spatial interpolation methodologies in urban air pollution modeling: application for the greater area of metropolitan Athens, Greece. Advanced Air Pollution, 17, 341-362.
[https://doi.org/10.5772/17734]

-
Dominick, D., Juahir, H., Latif, M.T., Zain, S.M., Aris, A.Z. (2012) Spatial assessment of air quality patterns in Malaysia using multivariate analysis. Atmospheric Environment, 60, 172-181.
[https://doi.org/10.1016/j.atmosenv.2012.06.021]

-
Fan, J., Li, Q., Hou, J., Feng, X., Karimian, H., Lin, S. (2017) A spatiotemporal prediction framework for air pollution based on deep RNN. ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 4(4W2), 15-22.
[https://doi.org/10.5194/isprs-annals-IV-4-W2-15-2017]

-
Guo, H., Sahu, S.K., Kota, S.H., Zhang, H. (2019) Characterization and health risks of criteria air pollutants in Delhi, 2017. Chemosphere, 225, 27-34.
[https://doi.org/10.1016/j.chemosphere.2019.02.154]

-
Kerckhoffs, J., Hoek, G., Gehring, U., Vermeulen, R. (2021) Modelling nationwide spatial variation of ultrafine particles based on mobile monitoring. Environment International, 154(2), 106569.
[https://doi.org/10.1016/j.envint.2021.106569]

-
Kumar, N., Middey, A., Rao, P.S. (2017) Prediction and examination of seasonal variation of Ozone with meteorological parameter through artificial neural network at NEERI, Nagpur, India. Urban Climate, 20, 148-167.
[https://doi.org/10.1016/j.uclim.2017.04.003]

-
Li, J., Heap, A.D. (2011) A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecological Informatics, 6(3), 228-241.
[https://doi.org/10.1016/j.ecoinf.2010.12.003]

-
Li, J., Heap, A.D. (2014) Spatial interpolation methods applied in the environmental sciences: A review. Environmental Modelling & Software, 53, 173-189.
[https://doi.org/10.1016/j.envsoft.2013.12.008]

-
Manan, D.N.A., Aizuddin, A.N., Hod, R. (2018) Effect of Air Pollution and Hospital Admission: A Systematic Review. Annals of Global Health, 84(4), 670.
[https://doi.org/10.29024/aogh.2376]

-
Merklinger-Gruchala, A., Jasienska, G., Kapiszewska, M. (2017) Effect of Air Pollution on Menstrual Cycle Length - A Prognostic Factor of Women’s Reproductive Health. International Journal of Environmental Research and Public Health, 14(7), 816.
[https://doi.org/10.3390/ijerph14070816]

-
Mishra, D., Goyal, P. (2015) Development of artificial intelligence based NO2 forecasting models at Taj Mahal, Agra. Atmospheric Pollution Research, 6(1), 99-106.
[https://doi.org/10.5094/APR.2015.012]

-
Mortimer, K.M., Neas, L.M., Dockery, D.W., Redline, S., Tager, I.B. (2002) The effect of air pollution on inner-city children with asthma. European Respiratory Journal, 19(4), 699-705.
[https://doi.org/10.1183/09031936.02.00247102]

-
Nagendra, S.M.S., Khare, M. (2005) Modelling urban air quality using artificial neural network. Clean Technologies and Environmental Policy, 7(2), 116-126.
[https://doi.org/10.1007/s10098-004-0267-6]

-
Nagendra, S.M.S., Khare, M. (2006) Artificial neural network approach for modelling nitrogen dioxide dispersion from vehicular exhaust emissions. Ecological Modelling, 190(1-2), 99-115.
[https://doi.org/10.1016/j.ecolmodel.2005.01.062]

- Osseiron, N., Lindmeier, C. (2018) 9 out of 10 people worldwide breathe polluted air. https://www.who.int/news/item/02-05-2018-9-out-of-10-people-worldwide-breathe-polluted-air-but-more-countries-are-taking-action
-
Papaleonidas, A., Iliadis, L. (2013) Neurocomputing techniques to dynamically forecast spatiotemporal air pollution data. Evolving Systems, 4(4), 221-233.
[https://doi.org/10.1007/s12530-013-9078-5]

-
Qi, Y., Li, Q., Karimian, H., Liu, D. (2019) A hybrid model for spatiotemporal forecasting of PM2.5 based on graph convolutional neural network and long short-term memory. Science of the Total Environment, 664, 1-10.
[https://doi.org/10.1016/j.scitotenv.2019.01.333]

-
Rigol, J.P., Jarvis, C.H., Stuart, N. (2001) Artificial neural networks as a tool for spatial interpolation. International Journal of Geographical Information Science, 15(4), 323-343.
[https://doi.org/10.1080/13658810110038951]

-
Roy, M.P. (2021) Air pollution and Covid-19: experience from India. European Review for Medical and Pharmacological Sciences, 25(8), 3375–3376.
[https://doi.org/10.26355/eurrev_202104_25749]

-
Russo, A., Soares, A.O. (2014) Hybrid Model for Urban Air Pollution Forecasting: A Stochastic Spatio-Temporal Approach. Mathematical Geosciences, 46(1), 75-93.
[https://doi.org/10.1007/s11004-013-9483-0]

-
Singh, K.P., Gupta, S., Kumar, A., Shukla, S.P. (2012) Linear and nonlinear modeling approaches for urban air quality prediction. Science of the Total Environment, 426, 244-255.
[https://doi.org/10.1016/j.scitotenv.2012.03.076]

-
Singh, V., Singh, S., Biswal, A. (2021) Exceedances and trends of particulate matter (PM2.5) in five Indian megacities. Science of the Total Environment, 750, 141461.
[https://doi.org/10.1016/j.scitotenv.2020.141461]

-
Vicente-Serrano, S.M., Saz-Sánchez, M.A., Cuadrat, J.M. (2003) Comparative analysis of interpolation methods in the middle Ebro Valley (Spain): Application to annual precipitation and temperature. Climate Research, 24(2), 161-180.
[https://doi.org/10.3354/cr024161]

-
Wang, J., Song, G. (2018) A Deep Spatial-Temporal Ensemble Model for Air Quality Prediction. Neurocomputing, 314, 198-206.
[https://doi.org/10.1016/j.neucom.2018.06.049]

-
Wen, C., Liu, S., Yao, X., Peng, L., Li, X., Hu, Y., Chi, T. (2019) A novel spatiotemporal convolutional long short-term neural network for air pollution prediction. Science of The Total Environment, 654, 1091-1099.
[https://doi.org/10.1016/j.scitotenv.2018.11.086]

-
Wong, C.M., Ma, S., Hedley, A.J., Lam, T.H. (2001) Effect of air pollution on daily mortality in Hong Kong. Environmental Health Perspectives, 109(4), 335-340.
[https://doi.org/10.1289/ehp.01109335]

- WHO (World Health Organization) (2018) Ambient (outdoor) air pollution [Fact sheet]. https://www.who.int/news-room/fact-sheets/detail/ambient-(outdoor)-air-quality-and-health
-
Yeganeh, B., Hewson, M.G., Clifford, S., Tavassoli, A., Knibbs, L.D., Morawska, L. (2018) Estimating the spatiotemporal variation of NO2 concentration using an adaptive neuro-fuzzy inference system. Environmental Modelling & Software, 100, 222-235.
[https://doi.org/10.1016/j.envsoft.2017.11.031]

-
Zou, B., Wang, M., Wan, N., Wilson, J.G., Fang, X., Tang, Y. (2015) Spatial modeling of PM2.5 concentrations with a multifactoral radial basis function neural network. Environmental Science and Pollution Research, 22(14), 10395-10404.
[https://doi.org/10.1007/s11356-015-4380-3]